题目内容
如图,已知直角梯形COAB中,CB‖OA,以O为原点,建立平面直角坐标系,A、B、C的坐标分别为A(6,0)、B(3,4)、C(0,4),D为OA的中点,动点P在线段AB上沿A至 B的方向运动,速度为每秒1个单位,运动时间记为t秒.(1)动点P在从A到B的运动过程中,记△APD的面积为S,试写出S与t的函数关系式,指出自变量的取值范围,并求出S的最大值;
(2)在动点P从A到B的运动过程中,是否存在某个时刻,使得四边形PBCD为等腰梯形?若存在,求出此时t的值;若不存在,请说明理由.
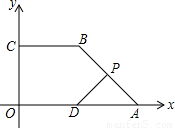
【答案】分析:(1)连接BD,过P作PE⊥OA于E,由D为OA中点可知AD=OD=BC=3,BD=CO=4,所以BC∥OD,BC=OD,再判断出四边形ODBC为矩形,在Rt△ABD中利用勾股定理求出AB的长,再由Rt△APE∽Rt△ABD可得出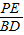 =
= ,
, ,进而得出PE的长,由三角形的面积即可得出结论;
,进而得出PE的长,由三角形的面积即可得出结论;
(2)因为BC∥AD,且BC=AD可得出四边形ABCD为平行四边形,由PB∥CD可知设在点P处四边形PBCD为等腰梯形,则PD=AD=BC=3.过D作DF⊥AB于F,AF=PF,再由DF=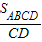 =
= 即可求出DF的长,再由勾股定理即可得出结论.
即可求出DF的长,再由勾股定理即可得出结论.
解答: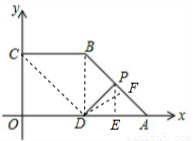 解:(1)连接BD,过P作PE⊥OA于E.
解:(1)连接BD,过P作PE⊥OA于E.
∵D为OA中点,
∴AD=OD=BC=3,BD=CO=4,
∴BC∥OD,BC=OD;
又∵∠DOC=90°,
∴四边形ODBC为矩形,
∴BD⊥OA,AB=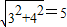 ,
,
∵Rt△APE∽Rt△ABD,
∴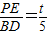 ,
,
∴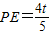 ,
,
∴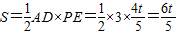 ,(0≤t≤5)
,(0≤t≤5)
∴当t=5时,S最大=6;
(2)存在.连接CD,由题意得:BC∥AD,且BC=AD
∴四边形ABCD为平行四边形,
∴PB∥CD.
设在点P处四边形PBCD为等腰梯形,则PD=AD=BC=3.
过D作DF⊥AB于F,则AF=PF,
又∵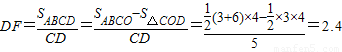 ,
,
∴ (秒)
(秒)
即此时t=3.6秒..
点评:本题考查的是相似三角形综合题及勾股定理,熟知相似三角形的判定与性质、勾股定理及等腰三角形的性质是解答此题的关键.
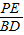 =
= ,
, ,进而得出PE的长,由三角形的面积即可得出结论;
,进而得出PE的长,由三角形的面积即可得出结论;(2)因为BC∥AD,且BC=AD可得出四边形ABCD为平行四边形,由PB∥CD可知设在点P处四边形PBCD为等腰梯形,则PD=AD=BC=3.过D作DF⊥AB于F,AF=PF,再由DF=
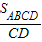 =
= 即可求出DF的长,再由勾股定理即可得出结论.
即可求出DF的长,再由勾股定理即可得出结论.解答:
 解:(1)连接BD,过P作PE⊥OA于E.
解:(1)连接BD,过P作PE⊥OA于E.∵D为OA中点,
∴AD=OD=BC=3,BD=CO=4,
∴BC∥OD,BC=OD;
又∵∠DOC=90°,
∴四边形ODBC为矩形,
∴BD⊥OA,AB=
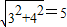 ,
,∵Rt△APE∽Rt△ABD,
∴
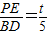 ,
,∴
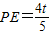 ,
,∴
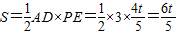 ,(0≤t≤5)
,(0≤t≤5)∴当t=5时,S最大=6;
(2)存在.连接CD,由题意得:BC∥AD,且BC=AD
∴四边形ABCD为平行四边形,
∴PB∥CD.
设在点P处四边形PBCD为等腰梯形,则PD=AD=BC=3.
过D作DF⊥AB于F,则AF=PF,
又∵
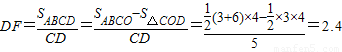 ,
,∴
 (秒)
(秒)即此时t=3.6秒..
点评:本题考查的是相似三角形综合题及勾股定理,熟知相似三角形的判定与性质、勾股定理及等腰三角形的性质是解答此题的关键.

练习册系列答案
相关题目
 如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.
如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED. 21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
 如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( ) 如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m.
如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m. 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.