题目内容
在条形统计图中,若各个小长方形的面积比为1:6:3:5,则用扇形统计图表示时,各扇形的圆心角度数分别为________.
24°,144°,72°,120°
分析:根据条形图中长方形的面积比求得各个量的比值为1:6:3:5,再求各个扇形的圆心角度数.
解答:由题意可知,各个量的比值为1:6:3:5
所以各个扇形的圆心角度数分别是

 360°=24°
360°=24°
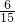 ×360°=144°
×360°=144°
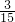 ×360°=72°
×360°=72°
 ×360°=120°.
×360°=120°.
点评:扇形统计图中,所表示的量的扇形所占圆的面积的百分比是它在总量中所占的百分比.所以该量所表示的扇形的圆心角度数是360度×它在总量中所占的百分比.本题的解题关键是根据条形图中长方形的面积比求得各个量的比值.
分析:根据条形图中长方形的面积比求得各个量的比值为1:6:3:5,再求各个扇形的圆心角度数.
解答:由题意可知,各个量的比值为1:6:3:5
所以各个扇形的圆心角度数分别是

 360°=24°
360°=24°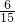 ×360°=144°
×360°=144°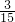 ×360°=72°
×360°=72° ×360°=120°.
×360°=120°.点评:扇形统计图中,所表示的量的扇形所占圆的面积的百分比是它在总量中所占的百分比.所以该量所表示的扇形的圆心角度数是360度×它在总量中所占的百分比.本题的解题关键是根据条形图中长方形的面积比求得各个量的比值.

练习册系列答案
相关题目
