Question

【题目】△ABC，∠A、∠B、∠C的对边分别是a、b、c，一条直线DE与边AC相交于点D，与边AB相交于点E．

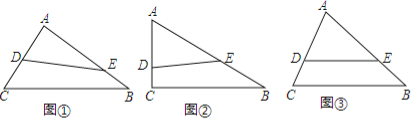
（1）如图①，若DE将△ABC分成周长相等的两部分，则AD+AE等于多少；（用a、b、c表示）

（2）如图②，若AC=3，AB=5，BC=4．DE将△ABC分成周长、面积相等的两部分，求AD；

（3）如图③，若DE将△ABC分成周长、面积相等的两部分，且DE∥BC，则a、b、c满足什么关系？

Answer 1

【答案】（1）（a+b+c)；（2）；（3）.

【解析】

试题分析：(1)因为DE将△ABC分成周长相等的两部分，所以AD+AE=CD+BC+BE=（AB+AC+BC）=（a+b+c），于是得出结论；(2)由题意可知△ABC为直角三角形，周长为12，面积为6，由上题结论可设AD=x，则AE=6﹣x，于是有S△ADE=ADAEsinA=3，即x（6﹣x）=3，解此方程，即可求得AD值；(3)

试题解析：（1）∵DE将△ABC分成周长相等的两部分，∴AD+AE=CD+BC+BE=（AB+AC+BC）=（a+b+c）；即AD+AE=（a+b+c)；（2）根据勾股定理的逆定理可知△ABC为直角三角形，由所给数据求得三角形ABC周长为12，面积为6，由上题结论可设AD=x，则AE=6﹣x，∵S△ADE=ADAEsinA=3，即：x（6﹣x）=3，解得：x1=（舍去），x2=，∴AD=；（3）∵DE∥BC，∴△ADE∽△ABC，∴，∵S△ADE:S△ABC=1：2,又因为面积比等于相似比的平方，∴AD=b，AE=c，∴b+c=（a+b+c），即（b+c)=a+b+c,整理得：.故a、b、c满足.