题目内容
 如图,点A(a,b)是抛物线
如图,点A(a,b)是抛物线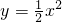 上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有
上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:过点A、B分别作x轴的垂线,通过构建相似三角形以及函数解析式来判断①②是否正确.△AOB的面积不易直接求出,那么可由梯形的面积减去构建的两个直角三角形的面积得出,根据得出的式子判断这个面积是否为定值.利用待定系数法求出直线AB的解析式,即可判断④是否正确.
解答: 解:过A、B分别作AC⊥x轴于C、BD⊥x轴于D,则:AC=b,OC=-a,OD=c,BD=d;
解:过A、B分别作AC⊥x轴于C、BD⊥x轴于D,则:AC=b,OC=-a,OD=c,BD=d;
(1)由于OA⊥OB,易知△OAC∽△BOD,有:
 =
= ,即
,即 =
=
∴ac=-bd(结论②正确).
(2)将点A、B的坐标代入抛物线的解析式中,有:
b= a2…Ⅰ、d=
a2…Ⅰ、d= c2…Ⅱ;
c2…Ⅱ;
Ⅰ×Ⅱ,得:bd= a2c2,即-ac=
a2c2,即-ac= a2c2,ac=-4(结论①正确).
a2c2,ac=-4(结论①正确).
(3)S△AOB=S梯形ACDB-S△ACO-S△BOD
= (b+d)(c-a)-
(b+d)(c-a)- (-a)b-
(-a)b- cd
cd
= bc-
bc- ad=
ad= (bc-
(bc- •
•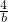 )=
)= (bc+
(bc+ )
)
由此可看出,△AOB的面积不为定值(结论③错误).
(4)设直线AB的解析式为:y=kx+h,代入A、B的坐标,得:
ak+h=b…Ⅲ、ck+h=d…Ⅳ
Ⅲ×c-Ⅳ×a,得:
h= =
= =-
=- ac=2;
ac=2;
∴直线AB与y轴的交点为(0,2)(结论④正确).
综上,共有三个结论是正确的,它们是①②④,故选C.
点评:题目涉及的考点并不复杂,主要有:利用待定系数法确定函数解析式、相似三角形的判定和性质以及图形面积的解法,难就难在式子的变形,可以将已知的条件列出,通过比较式子间的联系来找出答案.
分析:过点A、B分别作x轴的垂线,通过构建相似三角形以及函数解析式来判断①②是否正确.△AOB的面积不易直接求出,那么可由梯形的面积减去构建的两个直角三角形的面积得出,根据得出的式子判断这个面积是否为定值.利用待定系数法求出直线AB的解析式,即可判断④是否正确.
解答:
 解:过A、B分别作AC⊥x轴于C、BD⊥x轴于D,则:AC=b,OC=-a,OD=c,BD=d;
解:过A、B分别作AC⊥x轴于C、BD⊥x轴于D,则:AC=b,OC=-a,OD=c,BD=d;(1)由于OA⊥OB,易知△OAC∽△BOD,有:
 =
= ,即
,即 =
=
∴ac=-bd(结论②正确).
(2)将点A、B的坐标代入抛物线的解析式中,有:
b=
 a2…Ⅰ、d=
a2…Ⅰ、d= c2…Ⅱ;
c2…Ⅱ;Ⅰ×Ⅱ,得:bd=
 a2c2,即-ac=
a2c2,即-ac= a2c2,ac=-4(结论①正确).
a2c2,ac=-4(结论①正确).(3)S△AOB=S梯形ACDB-S△ACO-S△BOD
=
 (b+d)(c-a)-
(b+d)(c-a)- (-a)b-
(-a)b- cd
cd=
 bc-
bc- ad=
ad= (bc-
(bc- •
•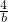 )=
)= (bc+
(bc+ )
)由此可看出,△AOB的面积不为定值(结论③错误).
(4)设直线AB的解析式为:y=kx+h,代入A、B的坐标,得:
ak+h=b…Ⅲ、ck+h=d…Ⅳ
Ⅲ×c-Ⅳ×a,得:
h=
 =
= =-
=- ac=2;
ac=2;∴直线AB与y轴的交点为(0,2)(结论④正确).
综上,共有三个结论是正确的,它们是①②④,故选C.
点评:题目涉及的考点并不复杂,主要有:利用待定系数法确定函数解析式、相似三角形的判定和性质以及图形面积的解法,难就难在式子的变形,可以将已知的条件列出,通过比较式子间的联系来找出答案.

练习册系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是