题目内容
已知:如图,在直角坐标系xoy中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,对角线 AC与OB相交于P,且BC=4,AB=6.
AC与OB相交于P,且BC=4,AB=6.
(1)求过点P的反比例函数的解析式;
(2)若该反比例函数的图象与AB交于点Q,求直线PQ的解析式.
解:
(1)∵四边形OABC都是矩形,对角线AC与OB相交于P
∴∠BAO=90°,点P为OB的中点
∵OA在x轴的负半轴上,OC在y轴的正半轴上,OA=BC=4,AB=6,
∴点B(-4,6)
∴点P(-2,3)
设过点P的反比例函数解析式为y=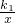 ,则
,则
3= ∴k1=-6.
∴k1=-6.
∴该反比例函数解析式为y= ;
;
(2)∵点Q在y= 图象上,当x=-4时,y=
图象上,当x=-4时,y=
∴点Q为(-4, ).
).
设过P、Q两点直线的解析式为y=k2x+b,把B(-2,3)Q(-4, ),代入得:
),代入得:
解得:
∴过P、Q两点直线的解析式为:y= .
.
分析:①要求解析式,首先要设出其函数关系式,为y=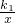 ,求出P点的坐标就可.
,求出P点的坐标就可.
②交AB于Q,有Q点的横坐标可以求出其纵坐标,即知道了Q点的坐标,再根据P点坐标可以直接求解.
点评:本题主要考查了反比例函数的性质,用待定系数法只需要知道其上面的一个点即可.同时要注意挖掘题目中的隐含条件.
(1)∵四边形OABC都是矩形,对角线AC与OB相交于P
∴∠BAO=90°,点P为OB的中点
∵OA在x轴的负半轴上,OC在y轴的正半轴上,OA=BC=4,AB=6,
∴点B(-4,6)
∴点P(-2,3)
设过点P的反比例函数解析式为y=
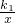 ,则
,则3=
 ∴k1=-6.
∴k1=-6.∴该反比例函数解析式为y=
 ;
;(2)∵点Q在y=
 图象上,当x=-4时,y=
图象上,当x=-4时,y=
∴点Q为(-4,
 ).
).设过P、Q两点直线的解析式为y=k2x+b,把B(-2,3)Q(-4,
 ),代入得:
),代入得:
解得:

∴过P、Q两点直线的解析式为:y=
 .
.分析:①要求解析式,首先要设出其函数关系式,为y=
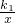 ,求出P点的坐标就可.
,求出P点的坐标就可.②交AB于Q,有Q点的横坐标可以求出其纵坐标,即知道了Q点的坐标,再根据P点坐标可以直接求解.
点评:本题主要考查了反比例函数的性质,用待定系数法只需要知道其上面的一个点即可.同时要注意挖掘题目中的隐含条件.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.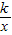 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
