题目内容
如图,已知A、B两点的坐标分别为(2| 3 |
(1)求点P的坐标;

(2)连BP、AP,在PB上任取一点E,连AE,将线段AE绕A点顺时针旋转90°到AF,连BF,交AP于点G,当E在线段BP上运动时,(不与B、P重合),求
| BE |
| PG |

分析:(1)连接BP、AP,过P作x轴的垂线,设垂足为Q;由圆周角定理知AB是⊙O的直径,而∠AOP=45°,
得出OP平分∠AOB,则弧BP=弧AP,由此可证得△ABP是等腰Rt△;易求得直径AB的长,即可求出AP的值;在Rt△APQ中,易知PQ=OQ,可用OQ表示出BQ,由勾股定理即可求得OQ、PQ的长,即可得出P点的坐标.
(2)先过F作FK⊥AP,再证明△AFK≌△EAP和△GFK≌△CBP,最后解出结果即可.
得出OP平分∠AOB,则弧BP=弧AP,由此可证得△ABP是等腰Rt△;易求得直径AB的长,即可求出AP的值;在Rt△APQ中,易知PQ=OQ,可用OQ表示出BQ,由勾股定理即可求得OQ、PQ的长,即可得出P点的坐标.
(2)先过F作FK⊥AP,再证明△AFK≌△EAP和△GFK≌△CBP,最后解出结果即可.
解答:解:(1)连接AP、BP,过P作PQ⊥x轴于Q;

∵∠AOB=90°,
∴AB是⊙O的直径,则∠APB=90°;
Rt△AOB中,OB=2,OA=2
,由勾股定理,得AB=4;
∵∠AOP=45°,
∴OP平分∠AOB,
∴弧BP=弧AP;
则△ABP是等腰Rt△,AP=2
;
Rt△POQ中,∠POQ=45°,则PQ=OQ;
设PQ=OQ=x,则AQ=2
-x;
Rt△APQ中,由勾股定理得:
AP2=AQ2+PQ2,即(2
-x)2+x2=8,
解得x=
+1,x=
-1(舍去),
∵∠POA=45°,∠PQO=90°,
∴PQ=OQ=x=
+1;
即P点坐标为(
+l,
+1);
(2)过F作FK⊥AP,则△AFK≌△EAP,

∴AK=PE,FK=AP=BP,
∴AP-AK=BP-PE,
∴PK=BE,
在△GFK和△GBP中,
∴△GFK≌△GBP,
∴PG=GK,
∴PG=
PK=
BE,
∴
=2;

∵∠AOB=90°,
∴AB是⊙O的直径,则∠APB=90°;
Rt△AOB中,OB=2,OA=2
| 3 |
∵∠AOP=45°,
∴OP平分∠AOB,
∴弧BP=弧AP;
则△ABP是等腰Rt△,AP=2
| 2 |
Rt△POQ中,∠POQ=45°,则PQ=OQ;
设PQ=OQ=x,则AQ=2
| 3 |
Rt△APQ中,由勾股定理得:
AP2=AQ2+PQ2,即(2
| 3 |
解得x=
| 3 |
| 3 |
∵∠POA=45°,∠PQO=90°,
∴PQ=OQ=x=
| 3 |
即P点坐标为(
| 3 |
| 3 |
(2)过F作FK⊥AP,则△AFK≌△EAP,

∴AK=PE,FK=AP=BP,
∴AP-AK=BP-PE,
∴PK=BE,
在△GFK和△GBP中,
|
∴△GFK≌△GBP,
∴PG=GK,
∴PG=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BE |
| PG |
点评:此题主要考查了圆周角定理、勾股定理、等腰直角三角形的判定和性质等知识的综合应用能力;能够构建出与已知和所求相关的直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
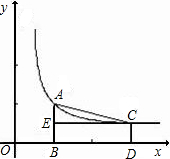 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(
如图,已知A、B两点的坐标分别为( 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论. 如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.
如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.