题目内容
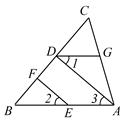
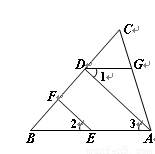
 如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.
请你完成下面的解题步骤:
解:因为EF∥AD,所以∠1=________.
又因为∠1=∠2,所以∠2=________.
所以AB∥________
所以∠BAC+________=180°.
因为∠BAC=68°,所以∠AGD=________.
∠3 ∠3 DG ∠AGD 112°
分析:由于EF∥AD,易得∠1=∠3,而∠1=∠2,等量代换可得∠2=∠3,可证AB∥DG,于是∠BAC+∠AGD=180°,进而可求∠AGD.
解答:∵EF∥AD,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.
∴AB∥DG
∴∠BAC+∠AGD=180°.
∵∠BAC=68°,∴∠AGD=112°.
故答案是∠3,3,DG,∠AGD,112°.
点评:本题考查了平行线的判定和性质.解题的关键是灵活掌握平行线的判定和性质.
分析:由于EF∥AD,易得∠1=∠3,而∠1=∠2,等量代换可得∠2=∠3,可证AB∥DG,于是∠BAC+∠AGD=180°,进而可求∠AGD.
解答:∵EF∥AD,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.
∴AB∥DG
∴∠BAC+∠AGD=180°.
∵∠BAC=68°,∴∠AGD=112°.
故答案是∠3,3,DG,∠AGD,112°.
点评:本题考查了平行线的判定和性质.解题的关键是灵活掌握平行线的判定和性质.

练习册系列答案
相关题目
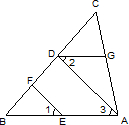 19、如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.
19、如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.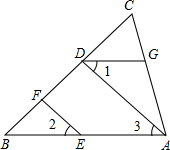 如图,已知EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.
如图,已知EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.