题目内容
如图，△ABC是等边三角形，D是AB的中点，以CD为一边向上作等边△ECD，连接AE，求证：△ADE是等腰三角形
证明:
∵△ABC是等边三角形
∴BC="AC " ∠ACB=600
同理，CD="CE" ∠DCE=600
∴∠ACB=∠DCE
∴∠DCB=∠ACE
在△BDC和△AEC中
BC=AC,
∠DCB=∠ACE
CD="CE"
∴△BDC≌△AEC（SAS）
∴BD="AE"
∵D为AB的中点
∴BD=AD
∴AD="AE " ∴△ADE是等腰三角形解析:
p;【解析】略
∵△ABC是等边三角形
∴BC="AC " ∠ACB=600
同理，CD="CE" ∠DCE=600
∴∠ACB=∠DCE
∴∠DCB=∠ACE
在△BDC和△AEC中
BC=AC,
∠DCB=∠ACE
CD="CE"
∴△BDC≌△AEC（SAS）
∴BD="AE"
∵D为AB的中点
∴BD=AD
∴AD="AE " ∴△ADE是等腰三角形解析:
p;【解析】略
练习册系列答案
综合自测系列答案
相关题目
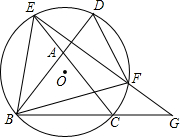∥AC，EF的延长线交BC的延长线于点G．
9、如图，△ABC是等边三角形，过AB边上一点D作BC的平行线交AC于E，则△ADE的三个内角
如图，△ABC是等边三角形，AB=4cm，则BC边上的高AD等于
如图，△ABC是等边三角形，D为BC边上的点，∠BAD=15°，将△ABD绕点A点逆时针方向旋转后到达△ACE的位置，那么旋转角的度数是
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．