题目内容
【题目】如图，已知正方形
的边长为
，
为
边上一点，
＝
．
（1）请直接写出AE的长是________；
（2）如图（1），若
为边
上的点，
与
相交于点
，且＝．求证：
；
（3）如图（2），若
为的中点，过点作直线分别与
，相交于点
、
，且
＝．请画出示意图并求出
长度．
【答案】（1）
；（2）见解析；（3）图见解析，2或3
【解析】
（1）根据正方形性质、勾股定理和含
锐角的直角三角形性质即可得到结论；
（2）根据正方形性质和题目条件可证明
，进而可得
；
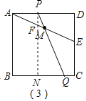
（3）分两种情况画出示意图（2）和（3），在图（2）中，根据正方形性质可先证明：四边形
为平行四边形，再利用勾股定理即可求得
，在图（3）中，先证明
，再利用勾股定理和等腰三角形性质即可求得．
解：（1）（1）
四边形
为正方形，
，
（2）如图
，∵ 四边形
为正方形，
∴ 
＝
，
＝
＝
，
在
和
中，
∴ 
，
∴ 
＝
＝
∵ 
＝
∴ 
＝
∴ 
＝
∴ 
；
（3）当如图（2）
时，过
作
，交
于点
，
∵ 四边形为正方形，
∴ ＝，
，
∴ 四边形
为平行四边形，
∴ 
＝
∵ ＝
∴ ＝
由（2）可得：
，
∴ 
，
∴ 
＝
∵ 
为的中点，
∴ 
，
设
＝
，在中，＝，
∴ 
＝
＝
，
根据勾股定理得：
＝
，即
，
∵ 
∴ ＝
，
∴ ＝＝
；
当如图
时，过
作
，交于点，交于点
，
同理可证：
，
∴ ＝
＝
∴ ＝
＝
∴ 
＝
在
中，＝，
∴ 
＝
，
∴ ＝
∴ 
，
根据勾股定理得：＝
综上可知，的长等于或．
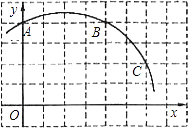
【题目】描点画图是探究未知函数图象变化规律的一个重要方法，下面是通过描点画图感知函数
图象的变化规律的过程：
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
| … |
（1）如表是________与________的几组对应值，则：m＝________；
（2）根据表中的数据，在平面直角坐标系
中描出还未描出的点，并画出该函数的图象：
（3）从函数图象可以看出，当________
时，________随着________的增大而________（填增大或减小）．
