题目内容
(1)计算:(- )-2-(-1)2010+(
)-2-(-1)2010+( )2009×(-
)2009×(- )2010;
)2010;
(2)[(x+2y)(x-2y)+4(x-y)2-7xy]÷(5x);
(3)已知a(a-1)-(a2-b)=4,求代数式 a2+
a2+ b2-ab的值.
b2-ab的值.
解:(1)原式=16-1+
=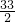 ;
;
(2)原式=(x2-4y2+4x2-8xy+4y2-7xy)÷(5x)
=(5x2-15xy)÷(5x)
=x-3y;
(3)∵a(a-1)-(a2-b)=4,
∴a-b=-4;
∴ a2+
a2+ b2-ab=
b2-ab= (a-b)2=
(a-b)2= ×16=8,即
×16=8,即 a2+
a2+ b2-ab=8.
b2-ab=8.
分析:(1)先计算指数幂,然后根据实数运算法则进行计算;
(2)先去括号,然后计算除法;
(3)根据已知条件求得a-b=-4;然后将所求的代数式转化为含有(a-b)的代数式的形式;最后将a-b代入求值即可.
点评:本题综合考查整式的混合运算、实数的运算以及负整数指数幂.解答(3)题时,采用了配方法化简代数式.根据配方法计算时,若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,则可先提取二次项系数,将其化为1后再计算.

=
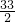 ;
;(2)原式=(x2-4y2+4x2-8xy+4y2-7xy)÷(5x)
=(5x2-15xy)÷(5x)
=x-3y;
(3)∵a(a-1)-(a2-b)=4,
∴a-b=-4;
∴
 a2+
a2+ b2-ab=
b2-ab= (a-b)2=
(a-b)2= ×16=8,即
×16=8,即 a2+
a2+ b2-ab=8.
b2-ab=8.分析:(1)先计算指数幂,然后根据实数运算法则进行计算;
(2)先去括号,然后计算除法;
(3)根据已知条件求得a-b=-4;然后将所求的代数式转化为含有(a-b)的代数式的形式;最后将a-b代入求值即可.
点评:本题综合考查整式的混合运算、实数的运算以及负整数指数幂.解答(3)题时,采用了配方法化简代数式.根据配方法计算时,若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,则可先提取二次项系数,将其化为1后再计算.

练习册系列答案
相关题目
