Question

【题目】如图，点A，B在反比例函数（x＞0）的图象上，点C、D在反比例函数（k＞0）的图象上，AC//BD//y轴，已知点A、B的横坐标分别为1、2，若△OAC与△ABD的面积之和为3，那么k的值是（　　）

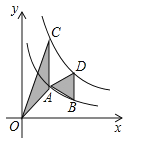
A. 5B. 4C. 3D. 2

Answer 1

【答案】A

【解析】

先分别表示出A、B、C、D的坐标，然后求出AC=k-1，BD=-，继而根据三角形的面积公式表示出S△AOC+S△ABD==3，解方程即可.

∵点A，B在反比例函数(x＞0)的图象上，点A、B的横坐标分别为1、2，

∴A(1，1)，B(2，)，

又∵点C、D在反比例函数(k＞0)的图象上，AC//BD//y轴，

∴C(1，)，D(2，)，

∴AC=k-1，BD=-，

∴S△AOC+S△ABD==3，

∴k=5，

故选A.