题目内容
已知实数x满足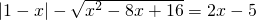
，求x的取值范围．
解：|1-x|-
=|1-x|-|x-4|
=x-1+x-4
=2x-5，
即1-x≤0且x-4≥0，
∴x≥4，
即x的取值范围是x≥4．
分析：先根据二次根式性质得出|1-x|-|x-4|，求出x-1+x-4即可得出2x-5，得出1-x≤0且x-4≥0，即可求出答案．
点评：本题考查了二次根式的性质和绝对值的应用，关键是能根据二次根式的性质和绝对值得出1-x≤0且x-4≥0．
=|1-x|-|x-4|
=x-1+x-4
=2x-5，
即1-x≤0且x-4≥0，
∴x≥4，
即x的取值范围是x≥4．
分析：先根据二次根式性质得出|1-x|-|x-4|，求出x-1+x-4即可得出2x-5，得出1-x≤0且x-4≥0，即可求出答案．
点评：本题考查了二次根式的性质和绝对值的应用，关键是能根据二次根式的性质和绝对值得出1-x≤0且x-4≥0．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
满足
，求代数式
的值. 
，求
的值．
满足
，求代数式 
的值.
，求
的值．
，求
的值．[来源:学+科+网Z+X+X+K]