题目内容
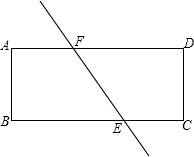
如图，直线a∥b，直线AC分别交a、b于点B、C，直线AD交a于点D．若∠1=20°，∠2=65°，则∠3度数等于
- A.30°
- B.45°
- C.60°
- D.85°
B
分析：先根据平行线的性质得出∠2=∠4，再根据三角形内角和外角的关系即可求出答案．
解答：
解：
∵直线a∥b，∴∠2=∠4，
又∵∠4=∠1+∠3，∴∠2=∠1+∠3，
∴∠3=∠2-∠1=65°-20°=45°．
故选B
点评：主要考查了三角形的内角和外角之间的关系以及平行线的性质．
三角形的外角等于与它不相邻的两个内角和．
分析：先根据平行线的性质得出∠2=∠4，再根据三角形内角和外角的关系即可求出答案．
解答：
解：∵直线a∥b，∴∠2=∠4，
又∵∠4=∠1+∠3，∴∠2=∠1+∠3，
∴∠3=∠2-∠1=65°-20°=45°．
故选B
点评：主要考查了三角形的内角和外角之间的关系以及平行线的性质．
三角形的外角等于与它不相邻的两个内角和．
练习册系列答案
阅读快车系列答案
相关题目
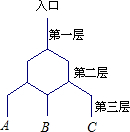如图所示是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有二条的为第二层，依此类推，现有一颗小弹子从第一层的通道里向下运动．并且小弹子落入每一条通道的可能性相同，则该小弹子从第三层通道的出口B脱出的概率为
