题目内容
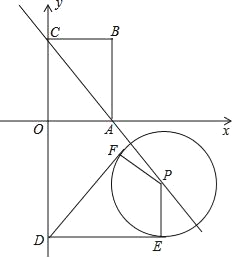
【题目】如图，在
中，
.点
在
轴的正半轴上，边AB在
轴上(点A在点B的左侧).
(1)求点C的坐标.
(2)点D是BC边上一点，点E是AB边上一点，且点E和点C关于AD所在直线对称，直接写出点D坐标.
【答案】(1)C(0，
)；(2)D(
，3).
【解析】
（1） 根据已知条件
可证△ABC是直角三角形，再用面积法求出OC长得到点C的坐标；
（2）先求出AE，得到OE,在利用三个三角形面积间的关系，得到
，再求出DE的长，即可确定点D的坐标
解：(1)在
中，
，
是直角三角形
由题意可知
点C的坐标为
(2)点D的坐标为
在Rt△AOC中， 
∵点E和点C关于AD所在直线对称
∴∠AED=∠ACD=90°，AE=AC=6,△AED≌△ACD
∴OE=AE-OA=
∵AE=6，AB=10
∴BE=4
∴
∴
∴
∴
即3DE=9
∴DE=3
∴D(，3).
练习册系列答案
相关题目
