题目内容
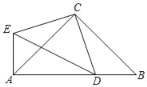
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=3![]() ,点D是斜边AB上一动点(点D与点A、B不重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接AE,DE.
,点D是斜边AB上一动点(点D与点A、B不重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接AE,DE.
(1)求△ADE的周长的最小值;
(2)若CD=4,求AE的长度.
【答案】(1)6+![]() ;(2)3﹣
;(2)3﹣![]() 或3+
或3+![]()
【解析】
(1)根据勾股定理得到AB=![]() AC=6,根据全等三角形的性质得到AE=BD,当DE最小时,△ADE的周长最小,过点C作CF⊥AB于点F,于是得到结论;
AC=6,根据全等三角形的性质得到AE=BD,当DE最小时,△ADE的周长最小,过点C作CF⊥AB于点F,于是得到结论;
(2)当点D在CF的右侧,当点D在CF的左侧,根据勾股定理即可得到结论
解:(1)∵在Rt△ABC中,∠ACB=90°,AC=BC=3![]()
∴AB=![]() AC=6,
AC=6,
∵∠ECD=∠ACB=90°,
∴∠ACE=∠BCD,
在△ACE与△BCD中, ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,
∴△ADE的周长=AE+AD+DE=AB+DE,
∴当DE最小时,△ADE的周长最小,
过点C作CF⊥AB于点F,

当CD⊥AB时,CD最短,等于3,此时DE=3![]() ,
,
∴△ADE的周长的最小值是6+3![]() ;
;
(2)当点D在CF的右侧,
∵CF=![]() AB=3,CD=4,
AB=3,CD=4,
∴DF=![]() ,
,
∴AE=BD=BF﹣DF=3﹣![]() ;
;
当点D在CF的左侧,同理可得AE=BD=3+![]() ,
,
综上所述:AE的长度为3﹣![]() 或3+
或3+![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(个) | 100 | 80 | 60 | … |
(1)求y与x之间的函数表达式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数表达式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?





