题目内容
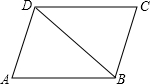
如图，∠ABD，∠ACD的角平分线交于点P，若∠A=50°，∠D=10°，则∠P的度数为
- A.15°
- B.20°
- C.25°
- D.30°
B
分析：利用角平分线的性质计算．
解答：
解：延长DC，与AB交于点E．
根据三角形的外角等于不相邻的两内角和，
可得∠ACD=50°+∠AEC=50°+∠ABD+10°，
整理得∠ACD-∠ABD=60°．
设AC与BP相交于O，则∠AOB=∠POC，
∴∠P+
∠ACD=∠A+∠ABD，
即∠P=50°-（∠ACD-∠ABD）=20°．
故选B．
点评：本题综合考查平分线的性质、三角形外角的性质、三角形内角和等知识点．
分析：利用角平分线的性质计算．
解答：
解：延长DC，与AB交于点E．根据三角形的外角等于不相邻的两内角和，
可得∠ACD=50°+∠AEC=50°+∠ABD+10°，
整理得∠ACD-∠ABD=60°．
设AC与BP相交于O，则∠AOB=∠POC，
∴∠P+
∠ACD=∠A+∠ABD，即∠P=50°-
（∠ACD-∠ABD）=20°．故选B．
点评：本题综合考查平分线的性质、三角形外角的性质、三角形内角和等知识点．
练习册系列答案
相关题目
4、如图，∠ABD=90°，直线
15、如图，∠ABD=∠CBD，DF∥AB，DE∥BC，则∠1与∠2的大小关系是
如图，△ABD中，点C、F分别为BD、AB上一点，AC、DF交于E，且CD=2BC，AE=2CE．求
如图，△ABD≌△ACE，那么点B与点
如图，△ABD≌△CDB，下面结论中不正确的是（ ）| A、△ABD和△CDB的面积相等 | B、∠A+∠ABD=∠C+∠CBD | C、△ABD和△CDB的周长相等 | D、AD∥BC，且AD=BC |