题目内容
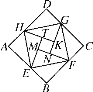
【题目】如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( ) 
A.AB⊥AC
B.AB=AC
C.AB=BC
D.AC=BC
【答案】B
【解析】解:AB=AC, 理由是:∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵D、F分别为AB和AC的中点,
∴DF∥BC,
∴AE⊥DF,
∵D、E、F分别是△ABC的边AB、BC、AC的中点,
∴EF∥AD,DE∥AF,
∴四边形ADEF是平行四边形,
∵AE⊥DF,
∴四边形ADEF是菱形,
即只有选项B的条件能推出四边形ADEF是菱形,选项A、C、D的条件都不能推出四边形ADEF是菱形,
故选B.
根据等腰三角形性质和三角形的中位线求出AE⊥DF,根据三角形的中位线求出DE∥AC,EF∥AB,得出四边形ADEF是平行四边形,再根据菱形的判定推出即可.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
【题目】某市中考体育测试有“跳绳”项目,为加强训练,某班女生分成甲、乙两组参加班级跳绳对抗赛,两组参赛人数相等,比赛结束后,依据两组学生的成绩(满分为10分)绘制了如下统计图表:
甲组学生成绩统计表
分 数 | 人 数 |
5分 | 5人 |
6分 | 2人 |
7分 | 3人 |
8分 | 1人 |
9分 | 4人 |

(1)经计算,乙组的平均成绩为7分,中位数是6分,请求出甲组学生的平均成绩、中位数,并从平均数的角度分析哪个组的成绩较好?
(2)经计算,甲组的成绩的方差是2.56,乙组的方差是多少?比较可得哪个组的成绩较为整齐?
(3)学校组织跳绳比赛,班主任决定从这次对抗赛中得分为9分的学生中抽签选取5个人组成代表队参赛,则在对抗赛中得分为9分的学生参加比赛的概率是多少?