题目内容
正 n 边形的内角和等于 1080°,那么这个正 n 边形的边数 n= .
8 .
【考点】多边形内角与外角.
【分析】n 边形的内角和是(n﹣2)•180°,如果已知多边形的内角和,就可以得到一个关于边数的 方程,解方程就可以求出多边形的边数.
【解答】解:设这个多边形是 n 边形,由题意知,
(n﹣2)×180°=1080°,
∴n=8. 故该多边形的边数为 8. 故答案为:8.
【点评】已知多边形的内角和求边数,可以转化为方程的问题来解决.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
阅读下面材料:
 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题:
|
小强的作法如下:
|
 老师说:“小强的作法正确.”
老师说:“小强的作法正确.”
请回答:小强用直尺和圆规作图 ,根据三角形全等的判定方法中的_______,
,根据三角形全等的判定方法中的_______,
得出△ ≌△
≌△ ,才能证明
,才能证明 .
.
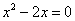 的解为
的解为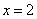 B.
B. 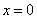 C.
C. 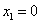 或
或 D.
D. 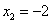
 +
+ )(
)(
