题目内容
如图，反比例函数的图象在第二象限内经过点A，过A作AP⊥x轴，垂足为P，连OA，若S△OPA=2，则此反比例函数解析式为
- A.
- B.
- C.
- D.
A
分析：设P的坐标是（m，n），则mn=k，可以利用m，n表示出三角形的面积，即可求得mn的值，进而求得k的值．
解答：设P的坐标是（m，n），则n=
，即k=mn，
∵OP=-m，AP=n，S△APO=
OA•OP=×（-m）n=-mn=2，
∴mn=-4，则k=-4．
则函数的解析式是：y=-
．
故选A．
点评：本题考查了反比例函数系数k的几何意义，过反比例函数图象上任意一点作x轴的垂线，垂线、坐标轴、以及点与原点的连线组成的直角三角形的面积是：|k|，利用点的坐标正确表示出三角形的面积是关键．本知识点是中考的重要考点，同学们应高度关注．
分析：设P的坐标是（m，n），则mn=k，可以利用m，n表示出三角形的面积，即可求得mn的值，进而求得k的值．
解答：设P的坐标是（m，n），则n=
，即k=mn，∵OP=-m，AP=n，S△APO=
OA•OP=×（-m）n=-mn=2，∴mn=-4，则k=-4．
则函数的解析式是：y=-
．故选A．
点评：本题考查了反比例函数系数k的几何意义，过反比例函数图象上任意一点作x轴的垂线，垂线、坐标轴、以及点与原点的连线组成的直角三角形的面积是：
|k|，利用点的坐标正确表示出三角形的面积是关键．本知识点是中考的重要考点，同学们应高度关注． 
练习册系列答案
相关题目
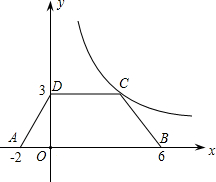（2012•南昌）如图，等腰梯形ABCD放置在平面坐标系中，已知A（-2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．
（2013•和平区一模）如图，反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）．
（2012•湖里区一模）如图，反比例函数y=
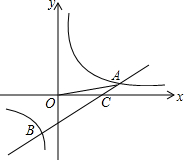已知：如图，反比例函数的图象和一次函数的图象交于A和B两点，且点A的坐标为（3，1），点B的坐标为（-1，-3），一次函数图象与X轴交于点C．连接OA．
的图象与直线
在第一象限交于点
，
为直线上的两点，点
的横坐标为2，点
的横坐标为3．
为反比例函数图象上的两点，且
平行于
轴．
的值；
的面积．