题目内容
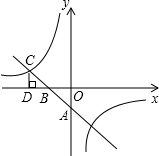 如图所示,一次函数与反比例函数的图象分别是直线AB和双曲线,直线AB与双曲线的一个交点为C,CD⊥x轴于点D,OD=2OB=4OA=4.
如图所示,一次函数与反比例函数的图象分别是直线AB和双曲线,直线AB与双曲线的一个交点为C,CD⊥x轴于点D,OD=2OB=4OA=4.(1)求一次函数的解析式;
(2)求反比例函数的解析式.
(提示:先求出一次函数的解析式,得到点C的坐标,从而求出反比例函数解析式)
分析:(1)通过OD=2OB=4OA=4,可求出A、B、C、D四点的坐标,又根据题意可知,点A、B在一次函数的图象上,利用待定系数法可求出a、b,从而得出一次函数的解析式;
(2)根据图象可知,C点的横坐标是-4,代入一次函数可求出其纵坐标,可得C点坐标,再代入反比例函数中可求出它的解析式.
(2)根据图象可知,C点的横坐标是-4,代入一次函数可求出其纵坐标,可得C点坐标,再代入反比例函数中可求出它的解析式.
解答:解:(1)设直线AB的解析式为y1=kx+b(k≠0),反比例函数的解析式为y2=
(k≠0),
由已知条件知OA=1,OB=2,OD=4,
则点A(0,-1),B(-2,0),D(-4,0),
把A(0,-1),B(-2,0),代入一次函数得
,
解得
,
故直线AB的解析式为y1=-
x-1;
(2)把D(-4,0),将x=-4代入一次函数得y1=-
×(-4)-1=1,
把x=-4,y=1代入反比例函数得解析式得-1=
,即k=-4,
故反比例函数的解析式为y2=-
.
| k |
| x |
由已知条件知OA=1,OB=2,OD=4,
则点A(0,-1),B(-2,0),D(-4,0),
把A(0,-1),B(-2,0),代入一次函数得
|
解得
|
故直线AB的解析式为y1=-
| 1 |
| 2 |
(2)把D(-4,0),将x=-4代入一次函数得y1=-
| 1 |
| 2 |
把x=-4,y=1代入反比例函数得解析式得-1=
| k |
| 4 |
故反比例函数的解析式为y2=-
| 4 |
| x |
点评:本题比较复杂信息量较大,关键是要根据信息求出各点的坐标,把所求结果代入相应的关系式.

练习册系列答案
相关题目
 如图所示,一次函数与反比例函数的图象分别是直线AB和双曲线,直线AB与双曲线的一个交点为C,CD⊥x轴于点D,OD=2OB=4OA=4.
如图所示,一次函数与反比例函数的图象分别是直线AB和双曲线,直线AB与双曲线的一个交点为C,CD⊥x轴于点D,OD=2OB=4OA=4.

 与反比例函数
与反比例函数 的图象相交于A,B两点,且与坐标轴的交点为
的图象相交于A,B两点,且与坐标轴的交点为 ,
, ,点B的横坐标为
,点B的横坐标为 .
.
 的解.
的解.