题目内容
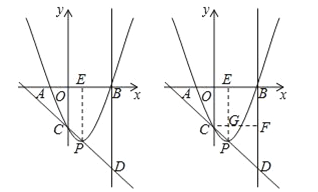
【题目】已知二次函数![]() (a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.

(1)求A、B两点的坐标;
(2)若tan∠PDB=![]() ,求这个二次函数的关系式.
,求这个二次函数的关系式.
【答案】(1)A(![]() ,0);(2)
,0);(2)![]() .
.
【解析】
试题分析:(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以OE:EB=CP:PD;
(2)过点C作CF⊥BD于点F,交PE于点G,构造直角三角形CDF,利用tan∠PDB=![]() 即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
试题解析:(1)过点P作PE⊥x轴于点E,∵![]() ,∴该二次函数的对称轴为:x=1,∴OE=1,∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=
,∴该二次函数的对称轴为:x=1,∴OE=1,∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=![]() ,∴OB=OE+EB=
,∴OB=OE+EB=![]() ,∴B(
,∴B(![]() ,0).∵A与B关于直线x=1对称,∴A(
,0).∵A与B关于直线x=1对称,∴A(![]() ,0);
,0);
(2)过点C作CF⊥BD于点F,交PE于点G,令x=1代入![]() ,∴y=c﹣a,令x=0代入
,∴y=c﹣a,令x=0代入![]() ,∴y=c,∴PG=a,∵CF=OB=
,∴y=c,∴PG=a,∵CF=OB=![]() ,∴tan∠PDB=
,∴tan∠PDB=![]() ,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴
,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴![]() ,∴PG=
,∴PG=![]() ,∴a=
,∴a=![]() ,∴
,∴![]() ,把A(
,把A(![]() ,0)代入
,0)代入![]() ,∴解得:c=﹣1,∴该二次函数解析式为:
,∴解得:c=﹣1,∴该二次函数解析式为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







