题目内容
已知点P是抛物线y=| 1 | 4 |
(1)猜想d1、d2的关系并证明;
(2)如果线段PQ的长度为5,求点M到x轴的最短距离.
分析:(1)本题可设出P点坐标,然后根据抛物线的解析式表示出d1,根据两点间的距离公式表示出d2,然后进行证明即可.
(2)本题要利用(1)的结论进行求解.过P、Q作x轴的垂线设垂足为P1、Q1.根据(1)的结论可以得出PP1=PF,QF=QQ1,如果过M作x轴的垂线MC,那么MC就是梯形PP1Q1Q的中位线,即MC=
(PP1+QQ1),如果MC最短,那么PP1+QQ1就需最短,而PP1=PF,QQ1=QF,因此PF+QF就必须最短,根据两点间线段最短可知当P、F、Q共线时,MC就最短,因此MC=
.
(2)本题要利用(1)的结论进行求解.过P、Q作x轴的垂线设垂足为P1、Q1.根据(1)的结论可以得出PP1=PF,QF=QQ1,如果过M作x轴的垂线MC,那么MC就是梯形PP1Q1Q的中位线,即MC=
| 1 |
| 2 |
| 5 |
| 2 |
解答:解:
(1)猜想d1=d2.
证明如下:
设P(x1,y1)是抛物线上任一点
∴d1=y1=
+1
而d2=PF=
=
=y1
∴d1=d2.
(2)过M作MC垂直x轴,垂足为C,易得MC=
(PP1+QQ1)
由(1)证PP1=PF,QQ1=QF
∴MC=
(PP1+QQ1),
即要求PF+QF最小值
而PF+QF≥PQ,
故当P、F、Q三点共线时,PF+QF最小,且等于PQ.
所以MC最小值为
,
即M到x轴最短距离为
.
(1)猜想d1=d2.
证明如下:
设P(x1,y1)是抛物线上任一点
∴d1=y1=
| x12 |
| 4 |
而d2=PF=
| x12+(y1-2)2 |
| 4y1-4+(y1-2)2 |
∴d1=d2.
(2)过M作MC垂直x轴,垂足为C,易得MC=
| 1 |
| 2 |
由(1)证PP1=PF,QQ1=QF
∴MC=
| 1 |
| 2 |
即要求PF+QF最小值
而PF+QF≥PQ,
故当P、F、Q三点共线时,PF+QF最小,且等于PQ.
所以MC最小值为
| 5 |
| 2 |
即M到x轴最短距离为
| 5 |
| 2 |
点评:本题主要考查了二次函数的应用、函数图象交点、中位线定理等知识点.

练习册系列答案
相关题目
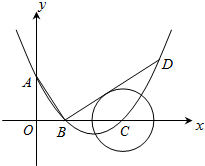 如图,在平面直角坐标系中,顶点为(4,-1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).
如图,在平面直角坐标系中,顶点为(4,-1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).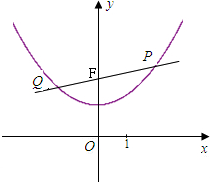 点P与点F(0,2)的距离为d2.
点P与点F(0,2)的距离为d2.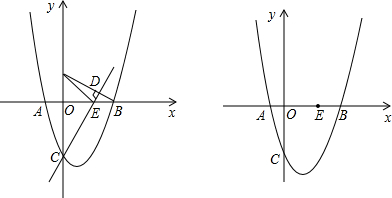
 (2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).
(2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).