��Ŀ����
����Ŀ����ͼ��������ABCD�У�AD��BC����B=90�㣬BC=6��AD=3����DCB=30�㣮��E��Fͬʱ��B�������������BC���������ƶ�����֪F���ƶ��ٶ���E���ƶ��ٶȵ�2������EFΪһ����CB���Ϸ����ȱߡ�EFG����E���ƶ�����Ϊx��x��0����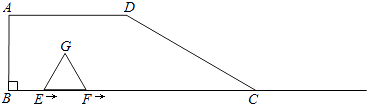
��1����EFG�ı߳������ú���x�Ĵ���ʽ��ʾ������x=2ʱ����G��λ������
��2������EFG������ABCD�ص����������y����y��x֮��ĺ�����ϵʽ��
��3��̽����2���еõ��ĺ���y��xȡ��ֵʱ���������ֵ����������ֵ��
���𰸡�
��1��x��D
��2��
�⣺�ٵ�0��x��2ʱ����EFG������ABCD�ڲ�������y= ![]() x2��
x2��
�ڷ����������
��2��x��3ʱ����ͼ1����E����F���߶�BC�ϣ�
��EFG������ABCD�ص�����Ϊ�ı���EFNM��
�ߡ�FNC=��FCN=30�㣬��FN=FC=6��2x����GN=3x��6��
����Rt��NMG�У���G=60�㣬GN=3x��6��
��GM= ![]() ��3x��6����
��3x��6����
�ɹ��ɶ����ã�MN= ![]() ��3x��6����
��3x��6����
��S��GMN= ![]() ��GM��MN=
��GM��MN= ![]() ��
�� ![]() ��3x��6����
��3x��6���� ![]() ��3x��6��=
��3x��6��= ![]() ��3x��6��2��
��3x��6��2��
���ԣ���ʱy= ![]() x2��
x2�� ![]() ��3x��6��2=��
��3x��6��2=�� ![]() ��
��

��3��x��6ʱ����ͼ2����E���߶�BC�ϣ���F������CH�ϣ�
��EFG������ABCD�ص�����Ϊ��ECP��
��EC=6��x��
��y= ![]() ��6��x��2=
��6��x��2= ![]() x2��
x2�� ![]() x+
x+ ![]() ��
��

��x��6ʱ����E��F�����߶�BC���ӳ����ϣ�û�������֣�
��y=0
��3��
�⣺��0��x��2ʱ��
��y= ![]() x2����x��0ʱ��y��x���������
x2����x��0ʱ��y��x���������
��x=2ʱ��y���= ![]() ��
��
��2��x��3ʱ����y=�� ![]() ��x=
��x= ![]() ʱ��y���=
ʱ��y���= ![]() ��
��
��3��x��6ʱ����y= ![]() ����x��6ʱ��y��x�������С��
����x��6ʱ��y��x�������С��
��x=3ʱ��y���= ![]() ��
��
������������x= ![]() ʱ��y���=
ʱ��y���= ![]() ��
��
���������⣺��1���ߵ�E��Fͬʱ��B�������������BC���������ƶ�����F���ƶ��ٶ���E���ƶ��ٶȵ�2����
��BF=2BE=2x��
��EF=BF��BE=2x��x=x��
���EFG�ı߳���x��
��D��DH��BC��H���þ���ABHD��ֱ�ǡ�CDH������DE��DF��
��ֱ�ǡ�CDH�У��ߡ�C=30�㣬CH=BC��AD=3��
��DH=CHtan30��=3�� ![]() ��x=2ʱ��BE=EF=2��
��x=2ʱ��BE=EF=2��
�ߡ�EFG�ǵȱ������Σ���DH��BC����H��
��EH=HF=1
��DE=DF= ![]() =2��
=2��
���DEF�ǵȱ������Σ�
���G��λ����D�㣮
�ʴ�Ϊx��D�㣻
��1�����ݵȱ������ε�������ȣ����EFG�ı߳��ǵ�E�ƶ��ľ��룻���ݵȱ������ε����ߺ�һ��F���ƶ��ٶ���E���ƶ��ٶȵ�2�������ɷ�����BF=4����ʱ�ȱ������εı߳���2�����G�͵�D�غϣ���2���ٵ�0��x��2ʱ���ص����ֵ������Ϊ�ȱ������ε�������ڵ�2��x��6ʱ���������������2��x��3ʱ�͵�3��x��6ʱ��x��6�����м��㣻��3���ֱ���ã�2����ÿһ����������ֵ���ٽ�һ���Ƚ�ȡ���е����ֵ���ɣ�