题目内容
 把一个矩形剪去一个正方形,所余的矩形与原矩形相似,那么原矩形的长与宽的比是
把一个矩形剪去一个正方形,所余的矩形与原矩形相似,那么原矩形的长与宽的比是分析:根据相似多边形对应边的比等于相似比,设出原来矩形的长和宽,就可得到关于长宽的方程,从而可以解得.
解答: 解:根据相似多边形对应边的成比例,
解:根据相似多边形对应边的成比例,
=
,
设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.
∴
=
解得:x=
y,或x=
(舍去).
∴
=
.
即原矩形的长与宽的比是
.
 解:根据相似多边形对应边的成比例,
解:根据相似多边形对应边的成比例,| AB |
| AE |
| AD |
| AB |
设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.
∴
| y |
| x-y |
| x |
| y |
解得:x=
1+
| ||
| 2 |
1-
| ||
| 2 |
∴
| x |
| y |
1+
| ||
| 2 |
即原矩形的长与宽的比是
1+
| ||
| 2 |
点评:根据相似多边形对应边的比相等,从而把几何问题转化为方程问题解决,解方程是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 略不计,如图2).设剪去的正方形边长为x(cm),x为正整数.折成的长方体盒子底面积为y(cm2).
略不计,如图2).设剪去的正方形边长为x(cm),x为正整数.折成的长方体盒子底面积为y(cm2).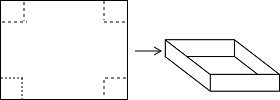 略不计,如图2).设剪去的正方形边长为x(cm),x为正整数.折成的长方体盒子底面积为y(cm2).
略不计,如图2).设剪去的正方形边长为x(cm),x为正整数.折成的长方体盒子底面积为y(cm2).