题目内容
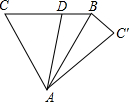 如图,过等边△ABC的顶点A,作一直线交BC于D,以AD为对称轴,将点C作轴对称变换,得点C′,连接AC′、BC′.若∠DAC=40°,则∠BAC′的度数是
如图,过等边△ABC的顶点A,作一直线交BC于D,以AD为对称轴,将点C作轴对称变换,得点C′,连接AC′、BC′.若∠DAC=40°,则∠BAC′的度数是
- A.15°
- B.20°
- C.25°
- D.40°
B
分析:根据∠BAC=60°,∠DAC=40°可得出,∠DAB的度数,再根据轴对称的性质可得∠CAD=∠DAC',从而可得出答案.
解答:∵△ABC是等边三角形,
∴∠DAC=40°,
又∵∠DAC=40°,
∴∠DAB=20°,
根据轴对称性质可得∠CAD=∠DAC'=40°,
∴∠BAC′=∠DAC'-∠DBA=20°.
故选B.
点评:本题考查轴对称的性质,属于基础题,解答本题的关键是根据题意得出关于某直线的对称的两个角,从而利用轴对称的性质进行解题.
分析:根据∠BAC=60°,∠DAC=40°可得出,∠DAB的度数,再根据轴对称的性质可得∠CAD=∠DAC',从而可得出答案.
解答:∵△ABC是等边三角形,
∴∠DAC=40°,
又∵∠DAC=40°,
∴∠DAB=20°,
根据轴对称性质可得∠CAD=∠DAC'=40°,
∴∠BAC′=∠DAC'-∠DBA=20°.
故选B.
点评:本题考查轴对称的性质,属于基础题,解答本题的关键是根据题意得出关于某直线的对称的两个角,从而利用轴对称的性质进行解题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (2013•吉安模拟)如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是( )
(2013•吉安模拟)如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是( )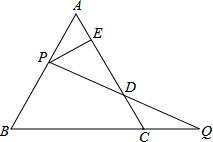 如图,过等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
如图,过等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.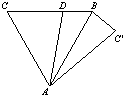 7、如图,过等边△ABC的顶点A,作一直线交BC于D,以AD为对称轴,将点C作轴对称变换,得点C′,连接AC′、BC′.若∠DAC=40°,则∠BAC′的度数是( )
7、如图,过等边△ABC的顶点A,作一直线交BC于D,以AD为对称轴,将点C作轴对称变换,得点C′,连接AC′、BC′.若∠DAC=40°,则∠BAC′的度数是( )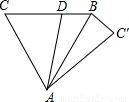 如图,过等边△ABC的顶点A,作一直线交BC于D,以AD为对称轴,将点C作轴对称变换,得点C′,连接AC′、BC′.若∠DAC=40°,则∠BAC′的度数是( )
如图,过等边△ABC的顶点A,作一直线交BC于D,以AD为对称轴,将点C作轴对称变换,得点C′,连接AC′、BC′.若∠DAC=40°,则∠BAC′的度数是( )