题目内容
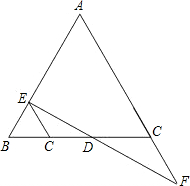
如图，DE∥AB，AC=3AD，S△ABC=5，则四边形ABED的面积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
分析：根据相似三角形的判定可得到△CDE∽△CAB，根据其相似比可求得其面积比，从而得到△CDE的面积，再根据则四边形ABED的面积=S△ABC-S△CDE即可得到答案．
解答：解：∵AC=3AD，
∴CD=2AD，
∴
=
，
∵DE∥AB，
∴△CDE∽△CAB，
∴面积的比等于（
）2=
，
∵S△ABC=5，
∴S△CDE=
，
∴四边形ABED的面积=5-
=
．
故选C．
∴CD=2AD，
∴
| CD |
| AC |
| 2 |
| 3 |
∵DE∥AB，
∴△CDE∽△CAB，
∴面积的比等于（
| 2 |
| 3 |
| 4 |
| 9 |
∵S△ABC=5，
∴S△CDE=
| 20 |
| 9 |
∴四边形ABED的面积=5-
| 20 |
| 9 |
| 25 |
| 9 |
故选C．
点评：本题考查相似三角形的性质的运用．
练习册系列答案
相关题目
（A类）如图，DE⊥AB、DF⊥AC．垂足分别为E、F．请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．
如图，DE∥AB，AC=2，CE=4，△ABC的面积是5，求△DCE的面积．
如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF
如图，DE⊥AB，EF∥AC，∠A=32°，求∠DEF的度数．
如图，DE⊥AB，∠A=25°，∠D=45°，则∠ACB的度数为