题目内容
平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为 ;Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为
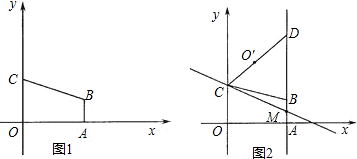
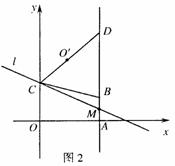
;Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为 ,且BC=5,AC=3(如图(1))
,且BC=5,AC=3(如图(1))
 ;Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为
;Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为 ,且BC=5,AC=3(如图(1))
,且BC=5,AC=3(如图(1))

(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动,D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s。
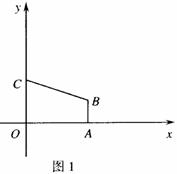
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图(1)、图(2)中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由。
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动,D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s。
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图(1)、图(2)中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由。
解:(1)由题意,设所求抛物线为y=a(x-3)2- ①, ①,将点(0,0)代入①,得a=  , ,∴y=  x2-3x; x2-3x;(2)①当点B位于原点左侧时,如图(1): S=S△OBD+S梯形OCAD-S△ABC =  ·4·(-m)+ ·4·(-m)+ (4+3)(5+m)- (4+3)(5+m)- = = m+10 m+10∴S=  m+10(-4.5≤m<0), m+10(-4.5≤m<0),当点B位于原点右侧(含原点O)时,如图(2): S=S梯形OCAD-S△OBD-S△ABC =  (4+3)(5+m)- (4+3)(5+m)- ·4·m- ·4·m- =  m+10, m+10,∴S=  m+10(0≤m< m+10(0≤m< -2); -2);②m1=-1,m2=-4,m3=-4.4。 |
  |

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目