题目内容
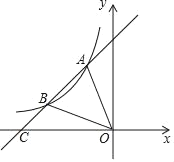
【题目】如图，在平面直角坐标系中，点
、
分别在
、
轴上，已知点的坐标为
，且
.
（1） （2） （3）
（1）求
的长度；
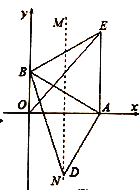
（2）以为一边作等边，过点作
，交
的垂直平分线
于点
.求证：
；
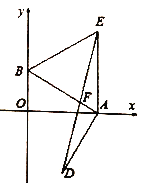
（3）在（2）的条件下，连接
交于
，求证：为的中点.
【答案】（1）
；（2）详见解析；（3）详见解析.
【解析】
（1）根据含30°的直角三角形的性质即可求解；
（2）连接
，得到
是等边三角形，故
，由
得到
，得到
是等边三角形，可证得
，即可求解；
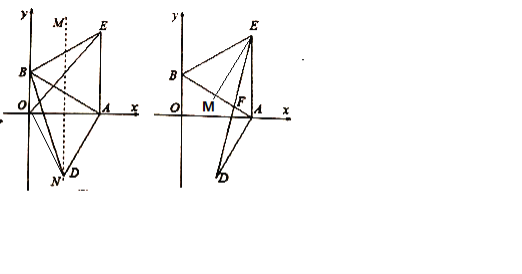
（3）过点
作
，根据是等边三角形，得到
，故
， 得到
，再证明
，即可求解.
解：（1）由点
的坐标（0,1），
，可得.
（2）
连接，是等边三角形，
，
，
又
，
，
，
是等边三角形，
，
，
（3）过点作，则
是等边三角形，
∴∠BAO=
又AB=EB,
，
∵EM∥AD,
∴∠MEF=∠ADF,又∠MFE=∠AFD
是
的中点.
练习册系列答案
名校课堂系列答案
相关题目
