Question

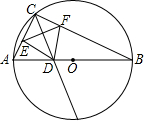
聪聪同学从小就喜欢动手动脑，请看他的研究：
①以AB为直径画⊙O；
②在⊙O上任取一点C；
③作∠ACB的角平分线与AB相交于点D；
④作CD的中垂线L与AC、BC分别相交于E、F；
⑤连接DE、DF．
如图，他发现：①∠ADE与∠BDF互余；  ②四边形CEDF为正方形；
③四边形CEDF的面积为AE•BF；④四边形CEDF的面积为常数．
你认为其中正确的是    ；（请填上所有正确答案的序号）

Answer 1

【答案】分析：根据线段垂直平分线上的点到线段两端的距离相等，可以证明CE=DE，CF=DF，再逆用等腰三角形三线合一的性质可得CE=CF，所以四边形CEDF四条边都相等，并且∠ACB是直角，所以四边形CEDF为正方形，然后根据正方形的四个角都是直角可以推出①正确，从而又可以证明△ADE与△DFB相似，根据相似三角形对应边成比例列出比例式，转化为乘积式即可证明③，利用极点法可以判断四边形CEDF的面积是随着点C的变化而变化的．
解答：解：根据题意，EF垂直平分CD，
∴CE=DE，CF=DF（线段垂直平分线上的点到线段两端点距离相等），
∵CD平分∠ACB，CD⊥EF，
∴CE=CF，
∴CE=DE=DF=FC，
∴四边形CEDF是菱形，
∵AB为⊙O的直径，点C在⊙O上，
∴∠ACB=90°（直径所对的圆周角是直角），
∴菱形CEDF是正方形，故②正确；
∴∠EDF=90°，
∴∠ADE+∠BDF=90°，
即∠ADE与∠BDF互余，故①正确；
又∵∠A+∠ADE=90°，
∴∠A=∠BDF，
在△ADE与△DFB中，，
∴△ADE∽△DFB，
∴=，
∴DE•DF=AE•BF，
正方形CEDF的面积=DE•DF=AE•BF，故③正确；
四边形CEDF的面积是随着点C变化而变化的，
当点C无限接近点A、B时，四边形CEDF的面积趋于0，当点CD过圆心O是面积最大，
∴四边形CEDF的面积不是常数，故④错误．
所以①②③正确．
故答案为：①②③．
点评：本题考查了相似三角形的判定与相似三角形的性质，线段垂直平分线的性质，直径所对的圆周角是直角的性质，以及正方形的判定与性质，综合性较强，证明四边形CEDF是正方形是解得本题的关键，突破口．