题目内容
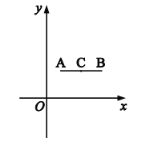
【题目】在平面坐标系![]() 中,已知线段
中,已知线段![]() ,且
,且![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(1)线段![]() 与
与![]() 轴的位置关系是
轴的位置关系是
(2)求点![]() 的坐标。
的坐标。
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得三角形
,使得三角形![]() 面积为3.若存在,求出点
面积为3.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)平行;(2)![]() ;(3)点P的坐标为
;(3)点P的坐标为![]() 时,三角形
时,三角形![]() 的面积为3.
的面积为3.
【解析】
(1)因为A、B点的纵坐标相同,所以线段![]() 与
与![]() 轴平行;(2)点
轴平行;(2)点![]() 为线段
为线段![]() 的中点,所以点C的横坐标即为点A、B横坐标的中间值,纵坐标和点A、B相同;(3)假设在
的中点,所以点C的横坐标即为点A、B横坐标的中间值,纵坐标和点A、B相同;(3)假设在![]() 轴上存在点
轴上存在点![]() ,使得三角形
,使得三角形![]() 的面积为3求出AC长,则
的面积为3求出AC长,则![]() ,由此可求出P点的纵坐标,根据点P在y轴上可知其坐标.
,由此可求出P点的纵坐标,根据点P在y轴上可知其坐标.
解:(1)因为A、B点的纵坐标相同,所以线段![]() 与
与![]() 轴平行;
轴平行;
(2)![]() ,C是线段AB的中点,∴C点坐标为:
,C是线段AB的中点,∴C点坐标为:![]()
(3)在![]() 轴上存在点
轴上存在点![]() ,使得三角形
,使得三角形![]() 的面积为3.其理由如下:
的面积为3.其理由如下:
由(2)知:![]() ,
,
![]()
![]()
即:![]()
![]()
![]() 或
或![]() ,
,
∴P点坐标为:![]() 或
或![]() 时,三角形
时,三角形![]() 的面积为3.
的面积为3.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目