Question

如图，抛物线y=ax² + bx + c 交x轴于A、B两点，交y轴于点C，对称轴为直线x=1,已知：A(-1,0)、C(0,-3)。
（1）求抛物线y= ax² + bx + c 的解析式；
（2）求△AOC和△BOC的面积比；
（3）在对称轴上是否存在一个P点,使△PAC的周长最小。
若存在，请你求出点P的坐标；若不存在，请你说明理由。

Answer 1

（1）∵抛物线与x轴交于A(-1,0)、B两点,且对称轴为直线x=1，
∴点B的坐标为（3，0），∴可设抛物线的解析式为y= a（x+1）(x-3)
又∵抛物线经过点C(0,-3)，∴ -3=a（0+1）(0-3)
∴a=1,∴所求抛物线的解析式为y=（x+1）(x-3)，
即y=x2-2x-3 
（2）依题意，得OA=1,OB=3,
∴S△AOC∶S△BOC=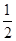OA·OC∶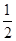OB·OC=OA∶OB=1∶3 
（3）在抛物线y=x2-2x-3上，存在符合条件的点P 。
解法1：如图，连接BC,交对称轴于点P,连接AP、AC。
∵AC长为定值，∴要使△PAC的 周长最小，只需PA+PC最小。
∵点A关于对称轴x=1的对称点是点B（3，0），
抛物线y=x2-2x-3与y轴交点C的坐标为（0，3）
∴由几何知识可知，PA+PC=PB+PC为最小。
设直线BC的解析式为y="kx-3" ,将B（3，0）代入得 3k-3="0" ∴k=1。
∴y="x-3" ∴当x=1时，y="-2" .∴点P的坐标为（1，-2） 
解法2：如图，连接BC,交对称轴于点P,连接AP、AC。设直线x=1交x轴于D
∵AC长为定值，∴要使△PAC的 周长最小，只需PA+PC最小。
∵点A关于对称轴x=1的对称点是点B（3，0），
抛物线y=x2-2x-3与y轴交点C的坐标为（0，3）
∴由几何知识可知，PA+PC=PB+PC为最小。
∵OC∥DP ∴△BDP∽△BOC 。∴即  
∴DP=2
∴点P的坐标为（1，-2）

解析