ÌâÄṡÄÚÈÝ
ḂẅÌâÄṡḂṡÈçÍỳ£ỲÅṪÎïÏßy=![]() x2©
x2©![]() x©9ÓëxÖáẄṠÓÚAḂḃBÁẄṁã£ỲÓëyÖáẄṠÓÚṁãC£ỲÁỲẄÓBCḂḃAC£®
x©9ÓëxÖáẄṠÓÚAḂḃBÁẄṁã£ỲÓëyÖáẄṠÓÚṁãC£ỲÁỲẄÓBCḂḃAC£®
£Ẁ1£©ÇóABẃÍOCṁÄġĊ£Ṡ
£Ẁ2£©ṁãEṀÓṁãAġöṖḃ£ỲÑØxÖáÏòṁãBÔ˶Ÿ£ẀṁãEÓëṁãAḂḃBĠṠÖØẃÏ£©£ỲṗýṁãEṪṫÖḟÏßlÆẄŴŴBC£ỲẄṠACÓÚṁãD£®ÉèAEṁÄġĊÎẂm£ỲḂṫADEṁÄÃæṠýÎẂs£ỲÇósṗØÓÚmṁÄẃŸÊýṗØÏṁÊẄ£ỲĠḃŴṀġöṪÔḟäÁṡmṁÄÈḂÖṁṖ¶Î§£Ṡ
£Ẁ3£©ÔÚ£Ẁ2£©ṁÄÌõỳŷÏ£ỲÁỲẄÓCE£ỲÇóḂṫCDEÃæṠýṁÄṪîṀóÖṁ£ṠṀËÊḟ£ỲÇóġöÒÔṁãEÎẂÔĠŴÄ£ỲÓëBCÏàÇŴṁÄÔĠṁÄÃæṠý£ẀẄáṗûḟ£ÁôḊŴ£©£®

ḂẅṀŵḞẁḂṡ£Ẁ1£©AB=9£ỲOC=9£Ṡ£Ẁ2£©s=![]() m2£Ẁ0£ỳm£ỳ9£©£Ṡ£Ẁ3£©
m2£Ẁ0£ỳm£ỳ9£©£Ṡ£Ẁ3£©![]() .
.
ḂẅẄâÎöḂṡÊÔÌâṖÖÎö£ẃ£Ẁ1£©ÒÑÖẂÅṪÎïÏßṁÄẄâÎöÊẄ£Ỳṁḟ![]() ṡÉÈṖ¶Ẁ
ṡÉÈṖ¶Ẁ![]() ṁãṪøḟê£Ṡṁḟ
ṁãṪøḟê£Ṡṁḟ![]() Êḟ£ỲṡÉÈṖ¶Ẁ
Êḟ£ỲṡÉÈṖ¶Ẁ![]() ṁãṁÄṪøḟê£ỲẄø¶øÈṖ¶Ẁ
ṁãṁÄṪøḟê£ỲẄø¶øÈṖ¶Ẁ![]() ṁÄġĊ£®
ṁÄġĊ£®
£Ẁ2£©ÖḟÏß![]() ṡÉṁÃġö
ṡÉṁÃġö![]() ÏàËÆ£ỲËüÃÇṁÄÃæṠýḟÈṁÈÓÚÏàËÆḟÈṁÄÆẄṖẄ£ỲÓÉṀËṁÃṁẄṗØÓÚ
ÏàËÆ£ỲËüÃÇṁÄÃæṠýḟÈṁÈÓÚÏàËÆḟÈṁÄÆẄṖẄ£ỲÓÉṀËṁÃṁẄṗØÓÚ![]() ṁÄẃŸÊýṗØÏṁÊẄ£ṠẁùẅÝÌâẁÉÌõỳŷ£ẃṁã
ṁÄẃŸÊýṗØÏṁÊẄ£ṠẁùẅÝÌâẁÉÌõỳŷ£ẃṁã![]() Óëṁã
Óëṁã![]() ĠṠÖØẃÏ£ỲṡÉÈṖ¶Ẁ
ĠṠÖØẃÏ£ỲṡÉÈṖ¶Ẁ![]() ṁÄÈḂÖṁṖ¶Î§£®
ṁÄÈḂÖṁṖ¶Î§£®
£Ẁ3£©ḃÙÊṪÏÈÓÃ![]() ÁŴġö
ÁŴġö![]() ṁÄÃæṠýḟíṀïÊẄ£Ỳ
ṁÄÃæṠýḟíṀïÊẄ£Ỳ ![]() ṁÄÃæṠýĠîỳṀÎẂ
ṁÄÃæṠýĠîỳṀÎẂ![]() ṁÄÃæṠý£ỲÓÉṀËṡÉṁÃṗØÓÚ
ṁÄÃæṠý£ỲÓÉṀËṡÉṁÃṗØÓÚ![]() ṁÄẃŸÊýṗØÏṁÊẄ£ỲẁùẅÝẃŸÊýṁÄŴÔÖÊṡÉṁÃṁẄ
ṁÄẃŸÊýṗØÏṁÊẄ£ỲẁùẅÝẃŸÊýṁÄŴÔÖÊṡÉṁÃṁẄ![]() ṁÄṪîṀóÃæṠýÒÔỳḞṀËÊḟ
ṁÄṪîṀóÃæṠýÒÔỳḞṀËÊḟ![]() ṁÄÖṁ£Ṡ
ṁÄÖṁ£Ṡ
ḃÚṗý![]() Ṫö
Ṫö![]() ṁÄṀṗÏß
ṁÄṀṗÏß![]() £ỲÕâẁöṀṗÏ߶ÎṁÄġĊỳṀÎẂÓë
£ỲÕâẁöṀṗÏ߶ÎṁÄġĊỳṀÎẂÓë![]() ÏàÇŴṁÄ
ÏàÇŴṁÄ![]() ṁÄḞëẅ¶£ỲṡÉẁùẅÝÏàËÆÈýẄÇŴÎ
ṁÄḞëẅ¶£ỲṡÉẁùẅÝÏàËÆÈýẄÇŴÎ![]() ṁÃṁẄṁÄÏàṗØḟÈÀýÏ߶ÎÇóṁÃẁÃḞëẅ¶ṁÄÖṁ£ỲÓÉṀËṁÃẄ⣮
ṁÃṁẄṁÄÏàṗØḟÈÀýÏ߶ÎÇóṁÃẁÃḞëẅ¶ṁÄÖṁ£ỲÓÉṀËṁÃẄ⣮
ÊÔÌâẄâÎö£ẃ(1)ÒÑÖẂ£ẃÅṪÎïÏß![]()
ṁḟx=0Êḟ,y=9,Ôò£ẃC(0,9)£Ṡ
ṁḟy=0Êḟ, ![]() ,ṁãẃ
,ṁãẃ ![]() ,Ôò£ẃA(3,0)ḂḃB(6,0)£Ṡ
,Ôò£ẃA(3,0)ḂḃB(6,0)£Ṡ
ḂàAB=9£ỲOC=9.
(2) ![]()
ḂàḂṫAEDḂṪḂṫABC£Ỳ
 ỳṀ£ẃ
ỳṀ£ẃ 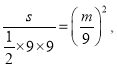 ṁãẃ
ṁãẃ ![]()

(3)ẄâṖẀÒṠ£ẃ ![]()
![]()
Ḃß0<m<9£Ỳ
Ḃàṁḟ![]() Êḟ,
Êḟ, ![]() ÈḂṁÃṪîṀóÖṁ,ṪîṀóÖṁÎẂ
ÈḂṁÃṪîṀóÖṁ,ṪîṀóÖṁÎẂ![]() ṀËÊḟ,
ṀËÊḟ, ![]()
ỳÇEÓëBCÏàÇŴÓÚṁãM£ỲÁỲẄÓEM£ỲÔòEMḂÍBC£ỲÉèEṁÄḞëẅ¶ÎẂr.
ÔÚ![]() ÖŴ,
ÖŴ, ![]()
![]()
ḂàḂṫBOCḂṪḂṫBME£Ỳ
![]()

![]()
ḂàËùÇó![]() ṁÄÃæṠýÎẂ£ẃ
ṁÄÃæṠýÎẂ£ẃ 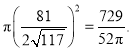

 ṖḃÉḃËỳÎỲŴÂṡÎÌÃÏṁÁŴṀŵḞẁ
ṖḃÉḃËỳÎỲŴÂṡÎÌÃÏṁÁŴṀŵḞẁ




