题目内容
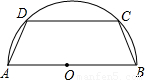
有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是圆O的直径，且底CD的端点在圆周上，试写出梯形周长y和腰长x的函数关系式分析：首先根据题意画出图形，根据垂径定理，可得辅助线OE⊥AD，根据三角函数的性质，即可求得AF的值，即可求得CD的值，问题的解．
解答：
解：过点O作OE⊥AD于E，过点D作DF⊥AB于F，
∴AE=DE=
x，
∴cosA=
=
=
，
∵cosA=
，
∴
=
，
∵AD=x，
∴AF=
，
∴CD=2OF=2（OA-AF）=2R-
，
∴周长y=2R+2x+CD=4R+2x-
．
故答案为：4R+2x-
．
解：过点O作OE⊥AD于E，过点D作DF⊥AB于F，∴AE=DE=
| 1 |
| 2 |
∴cosA=
| AE |
| OA |
| ||
| R |
| x |
| 2R |
∵cosA=
| AF |
| AD |
∴
| AF |
| AD |
| x |
| 2R |
∵AD=x，
∴AF=
| x2 |
| 2R |
∴CD=2OF=2（OA-AF）=2R-
| x2 |
| R |
∴周长y=2R+2x+CD=4R+2x-
| x2 |
| R |
故答案为：4R+2x-
| x2 |
| R |
点评：此题需要自己作图，比较难．此题考查了垂径定理与三角函数的性质，作出辅助线是此题的关键．
练习册系列答案
相关题目
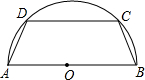（2007•安溪县质检）如图，有一块半径为5cm的半圆形钢板，计划截成等腰梯形ABCD的形状，他的下底AB是⊙O的直径，上底CD的端点在圆周上．
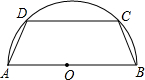如图，有一块半径为5cm的半圆形钢板，计划截成等腰梯形ABCD的形状，他的下底AB是⊙O的直径，上底CD的端点在圆周上．