题目内容
如图,在直角梯形ABCD中,∠D =∠BCD = 90°,∠B = 60°,AB = 6,AD = 9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G,如图①.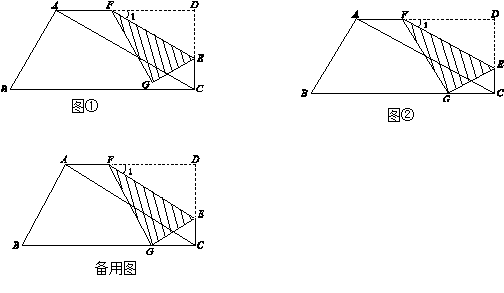
【小题1】求CD的长及∠1的度数;
【小题2】设DE = x,△GEF与梯形ABCD重叠部分的面积为y.
 求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?【小题3】当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移,速度为每秒1个单位,当E点移动到线段AB上时运动停止.设平移时间为t(秒),在平移过程中是否存在某一时刻t,使得△ABE为等腰三角形?若存在,求出t的值;若不存在,请说明理由
p;【答案】
【小题1】CD= ∠1=30°
∠1=30°
【小题2】Y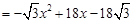
当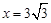 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为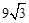
【小题3】①若AE=BE,解得t=9
②若AB=AE,解得t=9-2
③若BA=BE,解得t=12-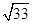 解析:
解析:
(1) 过点A作AH⊥BC于点H (1分)
∵在Rt△AHB中,AB=6,∠B=60°
∴AH=AB·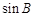 =
=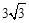
∵四边形ABCD为直角梯形
∴四边形AHCD为矩形
∴CD=AH=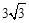 (2分)
(2分)
∵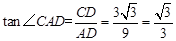
∴∠CAD=30°
∵EF∥AC
∴∠1=∠CAD=30° (4分)
(2)点G恰好在BC上,由对折的对称性可知△FGE≌△FDE
∴ GE="DE" =x,∠FEG=∠FED=60°
∴∠GEC=60°
因为△CEG是直角三角形
∴∠EGC="30°"
∴在Rt△CEG中,EC= EG=
EG= x
x
由DE+EC=CD 得
∴x=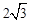 (5分)
(5分)
当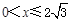 时
时
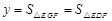
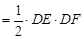
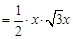

∵ >0,对称轴为y轴
>0,对称轴为y轴
∴当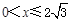 ,y随x的增大而增大
,y随x的增大而增大
∴当x= 时,
时,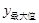 =
=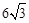 (6分)
(6分)
当 <x≤
<x≤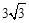 时,设FG,EG分别交BC于点M、N
时,设FG,EG分别交BC于点M、N
∵DE=x
∴EC=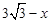 ,NE=2
,NE=2
∴NG=GE-NE= =
=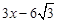
又∵∠MNG=∠ENC=30°,∠G=90°
∴MG= =
=
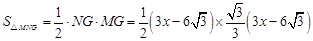



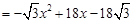 (7分)
(7分)
∵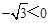 ,对称轴为直线
,对称轴为直线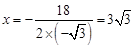
∴当 <x≤
<x≤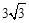 时,y有最大值
时,y有最大值
∴当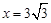 时,
时,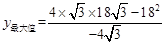 =
=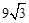 (8分)
(8分)
综合两种情形:由于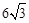 <
<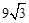
∴当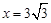 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为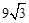 (9分)
(9分)
(3)由题意可知:AB=6,分三种情况:
①若AE=BE,解得t=9
②若AB=AE,解得t=9-2
③若BA=BE,解得t=12-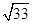 (12分)
(12分)
【小题1】CD=
 ∠1=30°
∠1=30°【小题2】Y
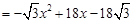
当
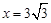 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为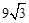
【小题3】①若AE=BE,解得t=9
②若AB=AE,解得t=9-2

③若BA=BE,解得t=12-
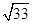 解析:
解析:(1) 过点A作AH⊥BC于点H (1分)
∵在Rt△AHB中,AB=6,∠B=60°
∴AH=AB·
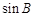 =
=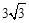
∵四边形ABCD为直角梯形
∴四边形AHCD为矩形
∴CD=AH=
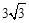 (2分)
(2分)∵
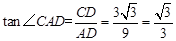
∴∠CAD=30°
∵EF∥AC
∴∠1=∠CAD=30° (4分)
(2)点G恰好在BC上,由对折的对称性可知△FGE≌△FDE
∴ GE="DE" =x,∠FEG=∠FED=60°
∴∠GEC=60°
因为△CEG是直角三角形
∴∠EGC="30°"
∴在Rt△CEG中,EC=
 EG=
EG= x
x由DE+EC=CD 得

∴x=
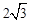 (5分)
(5分)当
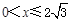 时
时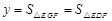
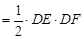
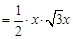

∵
 >0,对称轴为y轴
>0,对称轴为y轴∴当
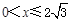 ,y随x的增大而增大
,y随x的增大而增大∴当x=
 时,
时,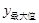 =
=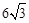 (6分)
(6分)当
 <x≤
<x≤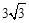 时,设FG,EG分别交BC于点M、N
时,设FG,EG分别交BC于点M、N∵DE=x
∴EC=
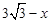 ,NE=2
,NE=2
∴NG=GE-NE=
 =
=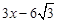
又∵∠MNG=∠ENC=30°,∠G=90°
∴MG=
 =
=
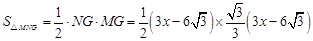



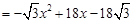 (7分)
(7分)∵
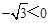 ,对称轴为直线
,对称轴为直线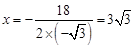
∴当
 <x≤
<x≤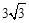 时,y有最大值
时,y有最大值∴当
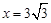 时,
时,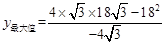 =
=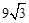 (8分)
(8分)综合两种情形:由于
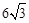 <
<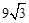
∴当
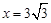 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为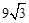 (9分)
(9分)(3)由题意可知:AB=6,分三种情况:
①若AE=BE,解得t=9
②若AB=AE,解得t=9-2

③若BA=BE,解得t=12-
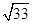 (12分)
(12分) 
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.