题目内容
有两根木条,长分别为6和8,现再截一根木条做一个钝角三角形,则第三根木条x长度的取值范围________.
10<x<14或
分析:已知三角形的两边长分别为6和8,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.注意本题做一个钝角三角形的要求.
解答:∵ =10,
=10,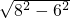 =2
=2 ,
,
6+8=14,8-6=2,
∴再截一根木条做一个钝角三角形,第三根木条x长度的取值范围 10<x<14或 .
.
故答案为:10<x<14或 .
.
点评:考查了三角形三边关系,本题需要理解的由勾股定理,根据已知的两条边求第三边的范围.

分析:已知三角形的两边长分别为6和8,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.注意本题做一个钝角三角形的要求.
解答:∵
 =10,
=10,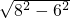 =2
=2 ,
,6+8=14,8-6=2,
∴再截一根木条做一个钝角三角形,第三根木条x长度的取值范围 10<x<14或
 .
.故答案为:10<x<14或
 .
.点评:考查了三角形三边关系,本题需要理解的由勾股定理,根据已知的两条边求第三边的范围.

练习册系列答案
相关题目
有两根木条,长分别为50cm和20cm,现在要选择第三根木条,将它们钉成一个三角形,设第三根木条的长为x cm,则x的取值范围是
[ ]
|
A.x>30 |
B.x<70 |
|
C.30<x<70 |
D.30≤x≤70 |