题目内容
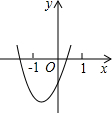已知抛物线y=ax2+bx+c（a≠0）如图．则abc________0，a-b+c________0，b2-4ac________0．
＜ ＜ ＞
分析：根据图象可确定a，b，c的符号，从而确定abc的符号；a-b+c是x=-1时的函数值；根据图象与x轴交点个数判断b2-4ac的符号．
解答：①∵图象开口向上，∴a＞0；
∵对称轴x=-
＜0，∴b＞0；
∵图象与y轴交点在负半轴，∴c＜0；
∴abc＜0．
②当x=-1时，y=a-b+c，根据图象知y＜0，所以a-b+c＜0．
③因为图象与x轴有两个交点，所以方程ax2+bx+c=0有两个不相等的实数根，则b2-4ac＞0．
故答案为：＜，＜，＞．
点评：此题考查了根据函数图象回答相关问题，重在熟练掌握图象所反映的信息．
分析：根据图象可确定a，b，c的符号，从而确定abc的符号；a-b+c是x=-1时的函数值；根据图象与x轴交点个数判断b2-4ac的符号．
解答：①∵图象开口向上，∴a＞0；
∵对称轴x=-
＜0，∴b＞0；∵图象与y轴交点在负半轴，∴c＜0；
∴abc＜0．
②当x=-1时，y=a-b+c，根据图象知y＜0，所以a-b+c＜0．
③因为图象与x轴有两个交点，所以方程ax2+bx+c=0有两个不相等的实数根，则b2-4ac＞0．
故答案为：＜，＜，＞．
点评：此题考查了根据函数图象回答相关问题，重在熟练掌握图象所反映的信息．
练习册系列答案
相关题目
与x轴的另一个交点为E．
如图，已知抛物线y=ax2+bx+c（其中b＞0，c＜0）的顶点P在x轴上，与y轴交于点Q，过坐标原点O，作OA⊥PQ，垂足为A，且OA=