��Ŀ����
����Ŀ����ͼ��������ABCD�У�AD��BC��AD=6cm��CD=8cm��BC=BD=10cm����P��B������BD���������˶����ٶ�Ϊ
1cm/s��ͬʱ���߶�EF��DC������DA���������˶����ٶ�Ϊ1cm/s����BD��Q������PE�������˶�ʱ��Ϊt��s����0��t��5��������������⣺

��1����tΪ��ֵʱ��PE��AB��
��2���Ƿ����ijһʱ��t��ʹS��DEQ=![]() �������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
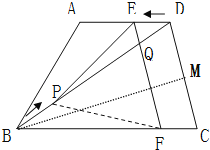
��3����ͼ2����PF���������˶������У������PFCDE������Ƿ����仯��˵�����ɣ�
���𰸡���1����t=![]() ��s��ʱ��PE��AB����2����t=2ʱ��S��DEQ=
��s��ʱ��PE��AB����2����t=2ʱ��S��DEQ=![]() ����3�����˶������У������PFCDE��������䣮
����3�����˶������У������PFCDE��������䣮
��������
�����������1����ҪPE��AB����Ӧ��![]() ������t��ʾDE��DP������ʽ���t��ֵ��
������t��ʾDE��DP������ʽ���t��ֵ��
��3������S��DEQ=![]() �������̣����t��ֵ��
�������̣����t��ֵ��
��4������PDE�ա�FBP������S�����PFCDE=S��PDE+S�ı���PFCD=S��FBP+S�ı���PFCD=S��BCD��������ε�������䣮
�⣺��1���������DE=BP=t����DP=10��t��
��PE��AB��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
����t=![]() ��s��ʱ��PE��AB��
��s��ʱ��PE��AB��
��2�����ڣ�
��DE��BC��
���DEQ�ס�BCD��
��![]() =��
=��![]() ��2��
��2��
��S��DEQ=![]() ��
��
��![]() =��
=��![]() ��2=
��2=![]() ��
��
����![]() ��2=
��2=![]() ��
��
��t2=![]() ��100=4��
��100=4��
t1=2��t2=��2������������ȥ����
����t=2ʱ��S��DEQ=![]() ��
��
��3�����䣮��B��BM��CD����CD��M
��S��BCD=![]() BM=
BM=![]() =8
=8![]() ��
��
����PDE����FBP��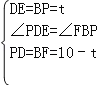 ��
��
���PDE�ա�FBP��
��S�����PFCDE=S��PDE+S�ı���PFCD=S��FBP+S�ı���PFCD=S��BCD=8![]() ��
��
�����˶������У������PFCDE��������䣮

 ��������������������ϵ�д�
��������������������ϵ�д�