题目内容
已知二次函数y=x2+ax+b的图象经过点（-2，-3），（2，5），求：
（1）此二次函数的关系式；
（2）设此函数图象与x轴交于A、B两点，顶点为M，求△AMB的面积；
（3）当x取何值时，y＞0．
解：（1）由题意可得：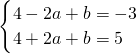
故
，
即y=x2+2x-3；
（2）令y=0得x2+2x-3=0，
∴x1=-3，x2=1，
∴AB=4，
顶点M的坐标为（-1，-4）故S=8；
（3）y＞0，即x2+2x-3＞0；
结合图象可得：
当x＜-3或x＞1时，y＞0．
分析：（1）将两点的坐标代入解析式可得a、b的值，即可得此二次函数的关系式；
（2）令y=0得x2+2x-3=0，解可得AB的横坐标，即可得AB的长度，再由M的横坐标，可得△AMB的面积；
（3）y＞0，即x2+2x-3＞0；结合词二次函数的图象可得答案．
点评：本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力．
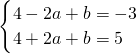
故
，即y=x2+2x-3；
（2）令y=0得x2+2x-3=0，
∴x1=-3，x2=1，
∴AB=4，
顶点M的坐标为（-1，-4）故S=8；
（3）y＞0，即x2+2x-3＞0；
结合图象可得：
当x＜-3或x＞1时，y＞0．
分析：（1）将两点的坐标代入解析式可得a、b的值，即可得此二次函数的关系式；
（2）令y=0得x2+2x-3=0，解可得AB的横坐标，即可得AB的长度，再由M的横坐标，可得△AMB的面积；
（3）y＞0，即x2+2x-3＞0；结合词二次函数的图象可得答案．
点评：本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．