题目内容
某公园有一圆弧形的拱桥,如图已知拱桥所在的圆的半径为10米,拱桥顶 到水面
到水面 距离
距离 米.
米.

(1)求水面宽度 的大小;
的大小;
(2)当水面上升到 时,从点
时,从点 测得桥顶
测得桥顶 的仰角为
的仰角为 ,若
,若 =3,求水面上升的高度.
=3,求水面上升的高度.
(1)16(2)2
【解析】解:(1)设拱桥所在圆的圆心为 ,由题意可知,点
,由题意可知,点 在
在 的延长线上,
的延长线上,
联结 ,
,
∵ ,
,
∴ (1分)
(1分)
在 中,
中, ,
,
∴ (2分)
(2分)
∵ ,
, 是半径,
是半径,
∴ (2分)
(2分)
即水面宽度 的长为
的长为 米.[来源:ZXXK]
米.[来源:ZXXK]
(2)设 与
与 相交于点
相交于点 ,联结
,联结 ,
,
∵
∴ ,
,
∴ ,
(1分)
,
(1分)
在 中,
中, ,
,
∴ (1分)
(1分)
设水面上升的高度为 米,即
米,即 ,则
,则 ,
,
∴
在 中,
中, ,
,
 , 化简得
, 化简得 
解得 (舍去),
(舍去), (2分)
(2分)
答:水面上升的高度为2米
(1)设拱桥所在圆的圆心为O,由题意可知,点O在DC的延长线上,连接OA,在Rt△ADO中利用勾股定理求出AD的长,再由垂径定理求出AB=2AC即可得出答案;
(2)设OD与EF相交于点G,连接OE,由EF∥AB,OD⊥AB,可知OD⊥EF,∠EGC=∠EGO=90°,在Rt△EGC中,由cotα=EG/CG =3,可知EG=3CG,设水面上升的高度为x米,即DG=x,则CG=4-x,则EG=12-3x,在Rt△EGO中,利用勾股定理即可求出x的值,进而得出结论.

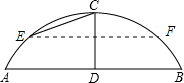 (2012•松江区二模)某公园有一圆弧形的拱桥,如图已知拱桥所在圆的半径为10米,拱桥顶D到水面AB的距离DC=4米.
(2012•松江区二模)某公园有一圆弧形的拱桥,如图已知拱桥所在圆的半径为10米,拱桥顶D到水面AB的距离DC=4米. 到水面
到水面 距离
距离 米.
米.
 时,从点
时,从点 测得桥顶
测得桥顶 ,若
,若 =3,求水面上升的高度.
=3,求水面上升的高度.
