题目内容

解方程：
（1） $数学公式$
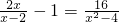
（2） $数学公式$ ．

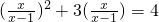解：（1）方程的两边同乘（x+2）（x-2），得
2x（x+2）-（x+2）（x-2）=16，
解得：x₁=-6，x₂=2，
检验：把x=-6代入（x+2）（x-2）≠0，即x=-6是原分式方程的解；
把x=-2代入（x+2）（x-2）=0，即x=-2不是原分式方程的解；
则原方程的解为：x=-6．

（2）令y= $\text{[math]}$ ，
原式可变为：y²+3y=4，
即（y-1）（y+4）=0，
解得：y₁=-4，y₂=1，
当 $\text{[math]}$ =-4时，解得：x= $\text{[math]}$ ；
当 $\text{[math]}$ =1时，此时无解；
经检验：x= $\text{[math]}$ 是原分式方程的解．
则原式分式方程的解为：x= $\text{[math]}$ ．
分析：（1）观察可得最简公分母是（x+2）（x-2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．
（2）利用换元法求解即可求得答案．
点评：此题考查了分式方程的求解方法．注意掌握转化思想的应用，注意解分式方程一定要验根．

练习册系列答案

导学新作业系列答案

学考新视野系列答案

学考英语阅读理解与完形填空系列答案

学考精练百分导学系列答案

学考传奇系列答案

学海乐园系列答案

星级口算天天练系列答案

世纪金榜初中全程复习方略系列答案

芒果教辅达标测试卷系列答案

轻松28套阳光夺冠系列答案

相关题目

17、解方程x²-|x|-2=0，
解：1．当x≥0时，原方程化为x²-x-2=0，解得：x₁=2，x₂=-1[不合题意，舍去]．
2．当x＜o时，原方程化为：x²+x-2=0，解得：x₁=1，（不合题意，舍去）x₂=-2．所以原方程的根为：x₁=2，x₂=-2
请参照例题解方程：x²-|x-1|-1=0

（1）解方程：4（x-1）=1-x
（2）解方程：

解方程：
x-

解：去分母，得6x-3x+1=4-2x+4…①
即-3x+1=-2x+8…②
移项，得-3x+2x=8-1…③
合并同类项，得-x=7…④
∴x=-7…⑤
上述解方程的过程中，是否有错误？答：

；如果有错误，则错在

步．如果上述解方程有错误，请你给出正确的解题过程．

计算与解方程：
（1）

计算下列各题：
（1）先化简再求值：

，（其中x=-3）．
（2）解方程