Question

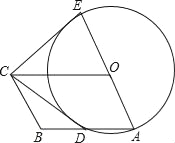
【题目】如图，在，，，垂足为，点是边上的一个动点，连接，过点作，交的延长线于点，连接交于点.

（1）请根据题意补全示意图；

（2）当与全等时，

①若，，，求的度数；

②试探究，，之间的数量关系，并证明.

Answer 1

【答案】（1）见解析（2）①40°②，，之间的数量关系为：

【解析】

（1）根据垂直画出图形即可得出结论；
（2）①先根据两三角形全等，判断出AB=DF，进而判断出BD=DE，再求出∠FDE=60°，进而利用三角形的外角的性质求出∠BDE=80°，进而求出∠DBE=∠BED=50°，即可得出结论；
②分两种情况：（ I）若BD=DE，先判断出∠DBE=∠DEB=β，进而得出∠FBG=180°-α-β，进而得出∠FBG=∠DGE，再判断出FB=FG，即可得出结论；
（ II）若AD=DE，先判断出DH＞DE，再判断出∠A=∠BID，进而得出∠BID＞∠C，即：∠A＞∠C，即可判断出此种情况不成立．

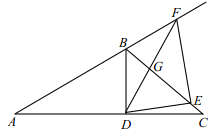
解：（1）如图即为所求示意图.

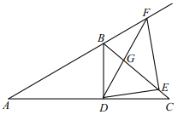
（2）①∵，，

∴.

∵与全等，

∴.

又∵，

∴，

.

在中，

∴.

∵，

∵，

∴.

∴.

∵，

∴.

在中，

.

②，，之间的数量关系为：.

证明：

由①得，.

（Ⅰ）若，

设，，

∵与全等，

∴.

∵，

∴.

∴.

在中，.

∴.

又∵，

∴.

∴.

又∵，

∴.

（Ⅱ）若，

如图，延长交于，

∵，

∴.

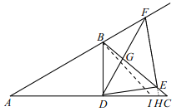
则在线段上存在点，使得.

连接，

∵，

又∵，

∴.

∴.

∵，

∴.

∴.

不符合题意.

综上所述，，，之间的数量关系为：.