题目内容
14.公共汽车经过一高地往返于A城和B城之间,上坡时它以25千米/小时的速度行驶,下坡时以50千米/小时的速度行驶,公共汽车从A城到B城要行驶$3\frac{1}{2}$小时,从B城到A城要行驶4小时,求出A城和B城之间的距离,并求出A城和B城至高地顶点C的距离.分析 设A到C为x千米,B到C为y千米,根据时间=$\frac{路程}{速度}$,列吃方程组,求出x,y的值,从而得出A城和B城至高地顶点C的距离,再把x,y的值相加即可得出A城和B城之间的距离.
解答 解:设A到C为x千米,B到C为y千米,根据题意得:
$\left\{\begin{array}{l}{\frac{x}{25}+\frac{y}{50}=3\frac{1}{2}}\\{\frac{x}{50}+\frac{y}{25}=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=75}\end{array}\right.$,
A城至高地顶点C的距离是50千米,B到C为75千米;
则A城和B城之间的距离是50+75=125(千米).
点评 此题考查了二元一次方程组的应用,用到的知识点是时间=$\frac{路程}{速度}$,关键是弄清题意,找出合适的等量关系,列出方程组.

练习册系列答案
相关题目
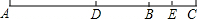 如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E是BC的中点.
如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E是BC的中点.