题目内容
如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.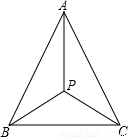
【答案】分析:把△ABP绕点A转到△ACP1,连接PP1,AP=AP1,PB=P1C,通过等腰三角形的性质,最后得出PC=P1C=PB,从而得证.
解答: 证明:如图,把△ABP绕点A转到△ACP1,连接PP1,
证明:如图,把△ABP绕点A转到△ACP1,连接PP1,
∵AB=AC,
∴AP=AP1,PB=P1C,∠APB=∠2+∠4=∠1+∠3,
∴∠1=∠2,
∴∠3=∠4,
∴PC=P1C=PB,
∴∠PBC=∠PCB.
点评:本题考查旋转的性质及等腰三角形的性质,解题关键是对旋转的熟练掌握及灵活应用.
解答:
 证明:如图,把△ABP绕点A转到△ACP1,连接PP1,
证明:如图,把△ABP绕点A转到△ACP1,连接PP1,∵AB=AC,
∴AP=AP1,PB=P1C,∠APB=∠2+∠4=∠1+∠3,
∴∠1=∠2,
∴∠3=∠4,
∴PC=P1C=PB,
∴∠PBC=∠PCB.
点评:本题考查旋转的性质及等腰三角形的性质,解题关键是对旋转的熟练掌握及灵活应用.

练习册系列答案
相关题目
 26、如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.
26、如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.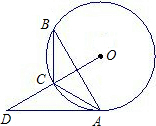 如图,△ABC内接于⊙O,D为OC延长线上一点,∠ABC=∠DAC=30°.
如图,△ABC内接于⊙O,D为OC延长线上一点,∠ABC=∠DAC=30°. 7、如图,△ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是CD上一点,且满足AD=DE,连接BD与AE相交于点F.求证:△ADF∽△ABC.
7、如图,△ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是CD上一点,且满足AD=DE,连接BD与AE相交于点F.求证:△ADF∽△ABC. 如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.
如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.