题目内容
如图，已知∠ABC是直角，在射线BC上取一点O为圆心、
BO为半径画圆，射线BA绕点B顺时针旋转________度时与⊙O相切，并说明理由．
60或120
分析：将射线BA绕点B顺时针旋转60°时，记为射线BE，作OD⊥BE，垂足为D，在直角三角形BOD中，证明圆心到直线的距离等于半径即可证得．
解答：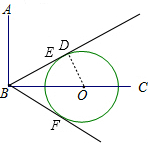
解：射线BA绕点B顺时针旋转60或120度时与圆O相切．
证明：将射线BA绕点B顺时针旋转60°时，记为射线BE，
作OD⊥BE，垂足为D，
∵在直角三角形BOD中，∠DBO=∠ABO-60°=30°，
∴OD=BO，即为⊙O的半径，
∴BE与⊙O相切．
射线BA绕点B顺时针旋转120°时，同理可证．
故答案是：60或120．
点评：本题主要考查了切线的判定，通过作辅助线转化为解直角三角形是解题的关键．
分析：将射线BA绕点B顺时针旋转60°时，记为射线BE，作OD⊥BE，垂足为D，在直角三角形BOD中，证明圆心到直线的距离等于半径即可证得．
解答：
解：射线BA绕点B顺时针旋转60或120度时与圆O相切．证明：将射线BA绕点B顺时针旋转60°时，记为射线BE，
作OD⊥BE，垂足为D，
∵在直角三角形BOD中，∠DBO=∠ABO-60°=30°，
∴OD=
BO，即为⊙O的半径，∴BE与⊙O相切．
射线BA绕点B顺时针旋转120°时，同理可证．
故答案是：60或120．
点评：本题主要考查了切线的判定，通过作辅助线转化为解直角三角形是解题的关键．
练习册系列答案
天天练口算系列答案
相关题目
的坐标为（-1，0）．
如图，已知△ABC是等边三角形，AB交⊙O于点D，DE⊥AC于点E．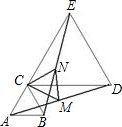
如图，已知△ABC是等边三角形，E是AC延长线上一点，选择一点D，使得△CDE是等边三角形，如果M是线段AD的中点，N是线段BE的中点，
（2012•襄城区模拟）如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．
（2013•奉贤区二模）如图，已知△ABC是等边三角形，点D是BC延长线上的一个动点，以AD为边作等边△ADE，过点E作BC的平行线，分别交AB，AC的延长线于点F，G，联结BE．