题目内容
【题目】如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;② ![]() =
= ![]() ;③S△PDQ=
;③S△PDQ= ![]() ;④cos∠ADQ=
;④cos∠ADQ= ![]() ,其中正确结论是(填写序号)
,其中正确结论是(填写序号) 
【答案】①②④
【解析】解:正确结论是①②④. 提示:①连接OQ,OD,如图1.
易证四边形DOBP是平行四边形,从而可得DO∥BP.
结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,
则有DQ=DA=1.
故①正确;②连接AQ,如图2.
则有CP= ![]() ,BP=
,BP= ![]() =
= ![]() .
.
易证Rt△AQB∽Rt△BCP,
运用相似三角形的性质可求得BQ= ![]() ,
,
则PQ= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
故②正确;③过点Q作QH⊥DC于H,如图3.
易证△PHQ∽△PCB,
运用相似三角形的性质可求得QH= ![]() ,
,
∴S△DPQ= ![]() DPQH=
DPQH= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
故③错误;④过点Q作QN⊥AD于N,如图4.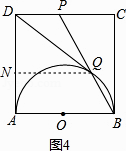
易得DP∥NQ∥AB,
根据平行线分线段成比例可得 ![]() =
= ![]() =
= ![]() ,
,
则有 ![]() =
= ![]() ,
,
解得:DN= ![]() .
.
由DQ=1,得os∠ADQ= ![]() =
= ![]() .
.
故④正确.
综上所述:正确结论是①②④.
所以答案是:①②④.
【考点精析】通过灵活运用平行四边形的判定与性质和平行线分线段成比例,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小
明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包
贴时没有重叠部分). 小明通过操作后发现此类包贴问题可将直三棱柱的
侧面展开进行分析.


(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是cm.