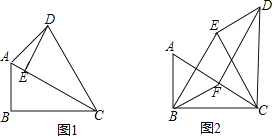
题目内容
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转120°到
顺时针旋转120°到![]() ,连接
,连接![]() ,连接
,连接![]() 并延长,分别交
并延长,分别交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)已知![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求菱形
,求菱形![]() 的面积.
的面积.
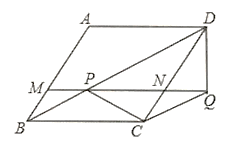
【答案】(1)证明见解析;(2)菱形![]() 的面积
的面积![]() .
.
【解析】
(1)利用SAS证明![]() ;
;
(2)先求出![]() ,得到
,得到![]() ,故当
,故当![]() 时,
时,![]() 最小,此时
最小,此时![]() 最小,根据MN=
最小,根据MN=![]() ,求出PC=2,BC=2PC=4,再利用菱形
,求出PC=2,BC=2PC=4,再利用菱形![]() 的面积
的面积![]() 得到答案.
得到答案.
(1)证明:四边形![]() 是菱形,且
是菱形,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
由旋转的性质得:![]()
∴![]() ,
,
∴![]() ;
;
(2)连接AC,
∵四边形ABCD是菱形,
∴AB=BC,
∵![]() ,
,
∴△ABC是等边三角形,
∴AB=BC,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 最小,此时
最小,此时![]() 最小,
最小,
∵MN=![]() ,
,
∴PC=2,
∵∠DBC=![]() ,∠BPC=90°,
,∠BPC=90°,
∴BC=2PC=4,
∴菱形![]() 的面积
的面积![]()


练习册系列答案
相关题目