题目内容
如图,点P为双曲线 上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线
上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线 于C、D,连接CD,若S△PCD=1,则k= .
于C、D,连接CD,若S△PCD=1,则k= .
【答案】分析:根据BC×BO=k,BP×BO=8,得出BC= BP,再利用AO×AD=k,AO×AP=8,得出AD=
BP,再利用AO×AD=k,AO×AP=8,得出AD= AP,进而求出
AP,进而求出 ×(1-
×(1- )PB×(1-
)PB×(1- )PA=
)PA= CP×DP=1,即可得出答案.
CP×DP=1,即可得出答案.
解答:解:∵点P为双曲线 上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线
上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线 于C、D,
于C、D,
∴PB×PA=8,
∵BC×BO=k,BP×BO=8,
∴BC= BP,
BP,
∵AO×AD=k,AO×AP=8,
∴AD= AP,
AP,
∴S△PCD= CP×DP=
CP×DP= ×(1-
×(1- )PB×(1-
)PB×(1- )PA=1,
)PA=1,
即是 ×(1-
×(1- )×(1-
)×(1- )×8=1,
)×8=1,
解得:k=4或12,
又k<8,
∴k=4.
故答案为:4.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出S△PCD= CP×DP=
CP×DP= ×(1-
×(1- )PB×(1-
)PB×(1- )PA=1是解决问题的关键.
)PA=1是解决问题的关键.
 BP,再利用AO×AD=k,AO×AP=8,得出AD=
BP,再利用AO×AD=k,AO×AP=8,得出AD= AP,进而求出
AP,进而求出 ×(1-
×(1- )PB×(1-
)PB×(1- )PA=
)PA= CP×DP=1,即可得出答案.
CP×DP=1,即可得出答案.解答:解:∵点P为双曲线
 上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线
上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线 于C、D,
于C、D,∴PB×PA=8,
∵BC×BO=k,BP×BO=8,
∴BC=
 BP,
BP,∵AO×AD=k,AO×AP=8,
∴AD=
 AP,
AP,∴S△PCD=
 CP×DP=
CP×DP= ×(1-
×(1- )PB×(1-
)PB×(1- )PA=1,
)PA=1,即是
 ×(1-
×(1- )×(1-
)×(1- )×8=1,
)×8=1,解得:k=4或12,
又k<8,
∴k=4.
故答案为:4.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出S△PCD=
 CP×DP=
CP×DP= ×(1-
×(1- )PB×(1-
)PB×(1- )PA=1是解决问题的关键.
)PA=1是解决问题的关键. 
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图、点A为双曲线上一点,AB⊥x轴,SOAB=3,则双曲线的解析式为( )
如图、点A为双曲线上一点,AB⊥x轴,SOAB=3,则双曲线的解析式为( )
 如图,点P为双曲线
如图,点P为双曲线 上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线
上一点,PA⊥x轴于A,PB⊥y轴于B,PA、PB分别交双曲线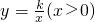 于C、D,连接CD,若S△PCD=1,则k=________.
于C、D,连接CD,若S△PCD=1,则k=________. 如图,点P为双曲线
如图,点P为双曲线 上一点,PA∥y 轴,PB∥x 轴,分别交双曲线
上一点,PA∥y 轴,PB∥x 轴,分别交双曲线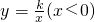 于A、B两点,且S四边形PAOB=3,则k=________.
于A、B两点,且S四边形PAOB=3,则k=________.