题目内容
 如图所示,A(-
如图所示,A(- ,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为
,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为
- A.

- B.

- C.

- D.2
C
分析:过P点作PD⊥x轴,垂足为D,根据A(- ,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用
,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用
S△ABP=S△AOB+S梯形BODP-S△ADP,列方程求a.
解答: 解:过P点作PD⊥x轴,垂足为D,
解:过P点作PD⊥x轴,垂足为D,
由A(- ,0)、B(0,1),得OA=
,0)、B(0,1),得OA= ,OB=1,
,OB=1,
∵△ABC为等边三角形,
由勾股定理,得AB= =2,
=2,
∴S△ABC= ×2×
×2× =
= ,
,
又∵S△ABP=S△AOB+S梯形BODP-S△ADP
= ×
× ×1+
×1+ ×(1+a)×3-
×(1+a)×3- ×(
×( +3)×a,
+3)×a,
= ,
,
由2S△ABP=S△ABC,得 =
= ,
,
∴a= .
.
故选C.
点评:本题考查了点的坐标与线段长的关系,不规则三角形面积的表示方法.
分析:过P点作PD⊥x轴,垂足为D,根据A(-
 ,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用
,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用S△ABP=S△AOB+S梯形BODP-S△ADP,列方程求a.
解答:
 解:过P点作PD⊥x轴,垂足为D,
解:过P点作PD⊥x轴,垂足为D,由A(-
 ,0)、B(0,1),得OA=
,0)、B(0,1),得OA= ,OB=1,
,OB=1,∵△ABC为等边三角形,
由勾股定理,得AB=
 =2,
=2,∴S△ABC=
 ×2×
×2× =
= ,
,又∵S△ABP=S△AOB+S梯形BODP-S△ADP
=
 ×
× ×1+
×1+ ×(1+a)×3-
×(1+a)×3- ×(
×( +3)×a,
+3)×a,=
 ,
,由2S△ABP=S△ABC,得
 =
= ,
,∴a=
 .
.故选C.
点评:本题考查了点的坐标与线段长的关系,不规则三角形面积的表示方法.

练习册系列答案
相关题目
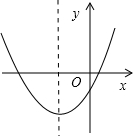 二次函数y=mx2+(6-2m)x+m-3的图象如图所示,则m的取值范围是( )
二次函数y=mx2+(6-2m)x+m-3的图象如图所示,则m的取值范围是( )| A、m>3 | B、m<3 | C、0≤m≤3 | D、0<m<3 |

 12、小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )
12、小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( ) 24、如图所示,向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2cm变成5cm时,圆形的面积从
24、如图所示,向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2cm变成5cm时,圆形的面积从 4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )
4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )