题目内容
【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
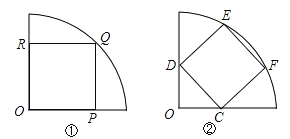
(3)探究:腰长为![]() 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
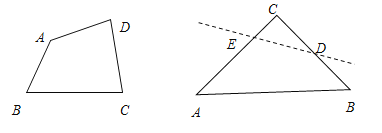
【答案】(1)正方形,菱形(写出一个即可) ;(2)对边之和相等;(3)有无数条 ;(4)![]() .
.
【解析】试题分析:(1)对角线平分每一对角的四边形都可以,如菱形、正方形;
(2)对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等;
(3)根据O到AB的距离等于O到DE的距离,即可得到答案;
(4)由勾股定理求出AB=2![]() ,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2
,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2![]() ,代入即可求出答案.
,代入即可求出答案.
试题解析:(1)答:一个有内心的四边形是菱形.
(2)答:对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等.
(3)解:有无数条,
理由是根据角平分线的性质得到:O到AB的距离等于O到DE的距离,在△ABC内有无数条,如图:具备DE∥AB即可.
(4)解:等腰直角三角形ACB,AC=BC=2,由勾股定理得:AB=2![]() ,
,
过D作DF⊥AB于F,过E作EQ⊥AB于Q,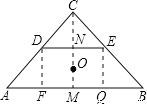

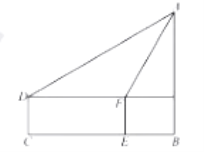
【题目】如图,点![]() ,
,![]() 之间有一条曲线和一条线段,
之间有一条曲线和一条线段,![]() 在线段
在线段![]() 上,己知
上,己知![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交曲线于点
交曲线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .设
.设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .(当点
.(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() )小思根据学习函数的经验,对函数
)小思根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
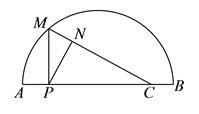
下面是小思的探究过程,请补充完整:
(![]() )通过取点,画图,测量,得到了
)通过取点,画图,测量,得到了![]() 与
与![]() 的几组值,补全下表:
的几组值,补全下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(说明:补全表格时相关数值保留一位小数)
(![]() )在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
)在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(![]() )结合画出的函数图象,解决问题:当
)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为__________
的长度约为__________![]() (结果保留一位小数).
(结果保留一位小数).