Question

【题目】在一节数学课上，老师布置了一个任务：

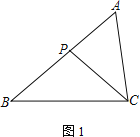
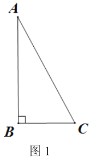
已知，如图1，在中，，用尺规作图作矩形．

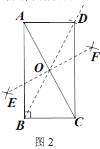
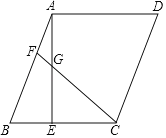
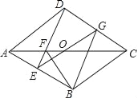
同学们开动脑筋，想出了很多办法，其中小亮作了图2，他向同学们分享了作法：

①分别以点、为圆心，大于长为半径画弧，两弧分别交于点、，连接交于点；

②作射线，在上取点，使；

③连接，．

则四边形就是所求作的矩形．

老师说：“小亮的作法正确．”

写出小亮的作图依据．

Answer 1

【答案】到线段两端距离相等的点在线段的垂直平分线上；直角三角形斜边上的中线等于斜边的一半；对角线互相平分且相等是矩形．

【解析】

根据到线段两端距离相等的点在线段的垂直平分线上可判断EF垂直平分AC，再根据直角三角形斜边上的中线等于斜边的一半得到BO＝OA＝OC，则由OD＝OB得到BO＝OA＝OC＝OD，从而根据矩形的判定方法可判断四边形ABCD就是所求作的矩形．

由作法得EF垂直平分AC，则OA＝OC，

则BO为Rt△ABC斜边上的中线，

所以BO＝OA＝OC，

因为OD＝OB，

所以BO＝OA＝OC＝OD，

所以四边形ABCD为矩形．

所以小亮的作图依据为：到线段两端距离相等的点在线段的垂直平分线上；直角三角形斜边上的中线等于斜边的一半；对角线互相平分且相等是矩形．